Az ABCD konvex négyszög AC és BD átlói 6 cm hosszúak és 45\r{ }-os szöget zárnak be az AB oldallal. Mekkora a négyszög területe?

Az $A$ csúcsból induló átló AB oldalnak ugyanazon az oldalán van, melyen $B$-ből induló, mert a két átló metszi egymást.. Nevezzük el a metszéspontot $O$-nak! Ekkor $O$ csúcsnál 180\r{ }-2*45\r{ } = 90\r{ } van az OAB háromszögben. Tehát az átlók merőlegesek egymásra, Egészítsük ki ábránkat! Húzzunk a csúcsokon át párhuzamost az átlókkal! Egy téglalapot kaptunk, hiszen a keletkezett négyszög oldalai merőlegesek egymásra. Mivel az átlók egyenlőek, ezért a téglalap oldalai is, tehát négyzet.

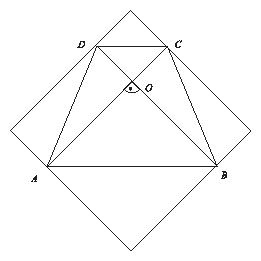
A négyzet területe 6cm*6cm = 36cm$^{2}$, a négyszög területe pedig ennek fele, 18cm$^{2}$, hiszen a négyzetet alkotó kis téglalapokat az átlójukkal megfeleztük, így kaptuk az ABCD négyszöget.