Adott a síkon nyolc pont úgy, hogy nincs közöttük négy egy egyenesen. Legfeljebb hány olyan egyenes van, amire az adott pontok közül három illeszkedik?

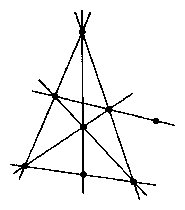
Az $ 1.$ ábra szerint 7 ilyen egyenes lehetséges. Megmutatjuk, hogy több "jó" egyenes nem lehet. Először is egy ponton háromnál több "jó" egyenes nem mehet át, különben a pontok száma nyolcnál több lenne, így a "jó" egyenesek száma legfeljebb $ 8\cdot 3/3=8$, hiszen ha a 8 pont mindegyikére legfeljebb 3 "jó" egyenes illeszkedik, akkor az legfeljebb 24 (nem feltétlenül különböző) "jó" egyenes, de minden "jó" egyenest háromszor számoltunk.

Legyen $A$ és $B$ olyan pont, hogy az AB egyenesen nincs további megadott pont! Vetítsük (centrálisan) a síkot egy ezen kívül fekvő $O$ pontból az OA, OB egyenesekkel párhuzamos síkra! Az $A$, illetve a $B$ pont képe ideális (végtelen távoli) pont, az ezekre illeszkedő "jó" egyenesek képe két különböző irányú 3--3 párhuzamos egyenesből álló alakzat ($ 2.$ ábra).

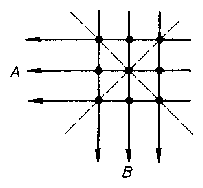
Az $A$ és a $B$ pontoktól különböző további 6 pont képének a 3--3 egyenes 9 (páronkénti) közös pontja között kell lennie. Ha volna 8 "jó" egyenes, úgy az $A$, illetve a $B$ képére illeszkedő, összesen 6 "jó" egyenesen kívül már csak két "átló" jöhet szóba, ez azonban ellentmondásra vezet, hiszen az előbbi 6 "jó" egyenes mindegyikére az $A$, illetve $B$ pontokon kívül pontosan két-két pont illeszkedik.
Megjegyzések: 1. A bizonyítás során felhasználtuk azt a tényt, hogy a 8 adott pont között van olyan kettő, amelyre illeszkedő egyenes nem tartalmaz további, megadott pontot. J. J. Sylvestertől ered még a múlt század végéről az a feladat, amelyet csak 1933-ban a magyar Gallai Tibornak sikerült bebizonyítania: Ha a sík n pontja nincs egyenesen, akkor létezik olyan egyenes, amely e pontok közül pontosan kettőt tartalmaz. Ugyanis, az $n$ számú $P_{1}$, $P_{2}$, {\ldots}, $P_{n}$ ponton át legfeljebb $n(n-1)/2$ olyan egyenest húzhatunk, amely a pontok közül két-két pontot tartalmaz. Tekintsük a ($P_{i}$; $P_{j}P_{k})$ párokat, amelyek egy pontból és egy arra nem illeszkedő egyenesből állanak. Mivel legfeljebb $(n-2)\cdot n(n-1)/2$ ilyen pár lehet, van közöttük legalább egy -- legyen az a ($P_{1}$; $P_{2}P_{3})$ --, amelyre a pontnak az egyenestől való $P_{1}Q$ távolsága az összes ilyen távolság köül a legkisebb ($ 3.$ ábra).

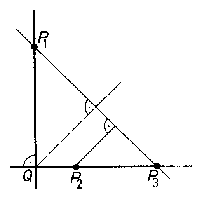
Ekkor a $P_{2}P_{3}$ egyenesen nincs további, adott pont. Ellenkező esetben, ha a $P_{4}$-gyel jelölhető adott pont is ezen az egyenesen van, úgy a $P_{1}Q$ egyenes egyik partján e három pont közül legalább kettő van (megengedve, hogy ezek egyike a $Q$ is lehet). Jelölje ezeket a $P_{2}$, illetve a $P_{3}$ és $P_2 QErdős Pál: Néhány elemi geometriai problémáról c. cikke, a Középiskolai Matematikai Lapok 61. (1980) számában, a 49-54. oldalakon. véges geometria egyik alapkérdése. Erről lásd például: Kárteszi Ferenc: Bevezetés a véges geometriákba, Akadémia Kiadó, 1972. c. művet.