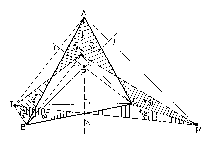
Legyen ABC egy hegyesszögű háromszög, $P$ pedig a háromszög egy belső pontja! A PAB, PBC, PCA háromszögek magasságpontját jelölje rendre $R$, $S$, $T$! Bizonyítsuk be, hogy az ABC és RST háromszögek területe megegyezik!

Mivel a háromszög hegyesszögű, ezért $M$ magasságpontja a háromszög belsejében van. Ha $P$ a háromszög $M$ magasságpontjával azonos, akkor igaz a feladat állítása, hiszen ekkor az $A$, $B$, $C$, $M$ pontnégyes ortocentrikus, vagyis közülük bármely három által kifeszített háromszög magasságpontja a negyedik, tehát a $P=M$ csúcsú háromszögek magasságpontjai az $A$, $B$ és $C$ pontok. A továbbiakban feltesszük, hogy $P\ne M$. Jelölje az $A$, $B$, $C$ csúcsokhoz tartozó magasságok talppontjait rendre $A'$, $B'$, illetve $C'$! Az $M$ kezdőpontú MA, MC', MB, MA', MC, MB' félegyenesek a síkot 6 szögtartományra bontják. Mivel $P\ne M$, akkor $P$ e szögtartományok legalább egyikéhez tartozik. Feltehető, hogy ez az AMC'$\angle $.

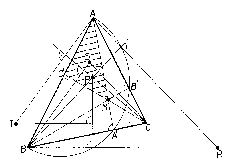
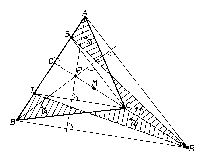
Ekkor az AMB háromszög tartalmazza az APB háromszöget, tehát ennek $A$, illetve $B$ csúcsához tartozó magasságvonalai az ABC háromszög külsejében vannak (e magasságok talppontjai az AB szakasz köré írt Thalész-körnek az ABC háromszög külsejéhez tartozó AB', illetve $A'B$ ívein vannak), és így $R$ az ABC háromszög külsejében van. A BPC háromszög tartalmazza a BMC háromszöget, tehát $S$ az ABC háromszöglemezhez tartozik, mert a BS, illetve CS félegyenesek kezdő szakaszai a PBA$\angle $, illetve ACP$\angle $ tartományokhoz tartoznak ($S$ az AB oldalon van, ha $P$ az MC' szakasz belső pontja). Végül az APC háromszög $T$ magasságpontja nem tartozhat az ABC háromszög belsejéhez, mert ellenkező esetben az AT magasságvonalának a CP egyenessel való közös pontjából, ami az ACC' derékszögű háromszög belső pontja, az AC szakasz tompaszögben látszana. ($T$ csak akkor tartozhat az ABC háromszög határához, ha $P$ az MC' szakasz belső pontja, tehát amikor az $S$ is a háromszög határán van.) Az ARCS és a CRBY négyszögek trapézok, hiszen AR, CS, illetve BR, CT oldalaik párhuzamosak, mivel a BP, illetve az AP egyenesre merőlegesek. Tudjuk, hogy egy trapéz átlói a trapézt négy olyan háromszögre darabolják, melyek közül a szárakon nyugvó két háromszög területe egyenlő. Ennélfogva az ABC és RST háromszögek egymásba átdarabolhatók ($ 2., 3.$ ábra), tehát területük egyenlő. (Az ábrákon az azonos számozású részek a fent említett trapézok egyenlő részei. A --, illetve a + jelek arra utaolnak, hogy az előbbi jelű részt az ABC háromszögből eltávolítjuk, s helyette az utóbbi, + jelű -- amazzal egyenlő területű -- részt pedig hozzávesszük.)