Az $AB$ körív $F$ felezőpontján átmenő egyenes a körívet másodszor az $F$ és $B$ közötti $M$ pontban metszi. Az $F$ pontból az $AM$ egyenesre állított merőleges talppontját jelölje $K$. Bizonyítsuk be, hogy $AK=\left( {AM+MB} \right)/2$.

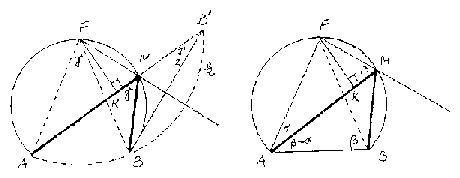
Mérjük fel az $AM$ szakasz $M$-en túli meghosszabbítására az $MB=MB\mbox{ }'$ szakaszt (1.~ábra), tehát $AB\mbox{ }'=AM+MB\mbox{ '}$. Mivel $BMB\mbox{ }'$ egyenlőszárú háromszög, ha $AMB\triangleleft =\gamma $, akkor $AB\mbox{ '}B\triangleleft =\gamma /2$. A kerületi szögek tételéből következik, hogy $AMB\triangleleft =AFB\triangleleft $, ezért az $F$ középpontú $FA=FB$ sugarú kör átmegy a $B\mbox{ '}$ ponton, $AB\mbox{ '}$ tehát a $k$ kör húrja és így középpontjából, $F$ -ből a rá emelt merőleges felezi $AB\mbox{ '}$-t, azaz

2. Megoldás

Legyen $FBA\triangleleft =FAB\triangleleft =\beta $, $FAM\triangleleft =\alpha $, ekkor $MAB\triangleleft =\beta -\alpha $(2.~ábra). Legyen a körív körének sugara $R$; felhasználjuk, hogy az $R$ sugarú körben a $\varphi $ kerületi szöghöz tartozó húr hossza $ 2R\sin \varphi $. Eszerint $FA=2R\sin \beta , \quad FM=2R\sin \alpha ,$ és $MB=2R\sin \left( {\beta -\alpha } \right)$ Az $M$ pont elhelyezkedése miatt $AM=AK+KM$ és az $AKF$ és $MKF$ derékszögű háromszögekből

A fentiek miatt a bizonyítandó egyenértékű az

állítással, ami a fenti trigonometrikus kifejezésekkel

alakba írható át, ebből átrendezéssel kapjuk, hogy

ami az ismert összegzési tétellel azonos. Állításunkat ezzel bebizonyítottuk. Megjegyzés. A feladat eredetijét az ókor nagy matematikusának, Archimédesznek tulajdonítják. További megoldásai a Középiskolai Mat. Lapok 1987. évi 10. számában (449{\-}451. old.) találhatók.