Egy derékszögű háromszög oldalainak mértékszámai egész számok. A háromszög területe mértékszámának kétszerese egyenlő a kerület mértékszámának háromszorosával. Mekkorák a háromszög oldalai?

Jelöljük a háromszög befogóit $a$ és $b$-vel, átfogóját $c$-vel. Feltehetjük, hogy a$<$b, ugyanis az egyenlő szárú derékszögű háromszögnek nem lehet mind a három oldala egész szám. Pitagorasz tétele szerint

a feladat követelménye szerint pedig

Meg kell határoznunk az , egyenletrendszer pozitív egész megoldásait, azaz meg kell oldanunk ezen diofantoszi egyenletrendszert. Ebben eljárhatunk úgy, hogy kiküszöböljük $c${\-}t, így egyetlen, az $a$ és $b$-ben szimmetrikus diofantoszi egyenletre jutunk - ugyanis és mindegyike $a$ és $b$-ben szimmetrikus -, ezt megoldjuk, majd a megoldások közül kiválasztjuk azokat, amelyekhez vagy szerint tartozó $c$ szintén egész szám. -ből

ezt -be helyettesítve, a törtek eltávolításával

majd rendezés után ab-vel végigosztva (ugyanis $a,\mbox{ }b\ne 0)$ az egyenletet így alakíthatjuk:

$a$ és $b$-vel együtt a bal oldal tényezői egészek. A jobb oldali szám hatféleképpen bontható fel két egész szám szorzatára: $ 1\cdot 18, \quad 2\cdot 9, \quad 3\cdot 6,$ továbbá $\left( {-1} \right)\cdot \left( {-18} \right)$, $\left( {-2} \right)\cdot \left( {-9} \right)$, $\left( {-3} \right)\cdot \left( {-6} \right)$. Mivel azonban $a$ és $b$ pozitívok, tehát $a$-6 és $b$-6 mindegyike nagyobb (-6)-nál, és ezt a követelményt 18 negatív egész tényezőpárjai közül egyik sem teljesíti egyidejűleg mindkét tényezőre, azért csak a pozitív tényezőkre bontások felelnek meg. Ezek szerint -nak három megoldása van:

Mivel 18-cal együtt az $a$-6 és $b$-6 tényezőknek legalább az egyike osztható 3-mal, azért ugyanez áll a 6-tal nagyobb $a$ és $b$-re és következésképpen szorzatukra is, ennélfogva a -ból kiszámítható $c$ mindhárom esetben egész szám: $c=$ 25, 17, 15. Ezek szerint a követelményeknek három háromszög felel meg. Megjegyzés: Néhány versenyző indokolatlanul feltételezte, hogy a keresett háromszög oldalainak aránya 3:4:5. Miután a megoldások között ilyen is van, így véletlenül ebből az alaptalan feltevésből is rá lehetett jutni egy megoldásra, de nem mindre.

2. Megoldás

Ismeretes, hogy minden háromszög területe $t=\rho \cdot s$ alakban írható, ahol $\rho $ a háromszög beírt körének sugara, és $s$ a háromszög félkerülete. Így a keresett háromszögre nézve $ 2\rho s=3\cdot 2s$, és innen, mivel $s$ nem lehet 0, $\rho $=3, egész szám. A beírt kör érintési pontjai az oldalakat úgy osztják két-két részre, hogy a csúcsokban összefutó részek páronként egyenlők. A derékszög csúcsában összefutó két rész hossza $\rho $, mert e részek és a végpontjaikhoz tartozó sugarak által alkotott négyszögben három derékszög van, és két szomszédos oldal egyenlő, tehát az idom négyzet. Eszerint, az átfogó két szakaszát $x$, $y$-nal jelölve az oldalak rendre:

tehát

egész számok. Pitagorasz tételével

ezt az egyenletet a következő alakra hozhatjuk:

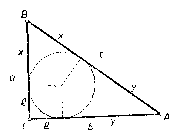
Eszerint ismét 18 egész tényezőpárokra bontásai vezetnek megoldáshoz. A beírt kör középpontja, a befogókon levő érintési pontok és az átfogó végpontjai által meghatározott derékszögű háromszögekből látható, hogy az $x$, $y$ befogók nagyobbak $\rho $-nál, mert velük szemben nagyobb szög fekszik. Ugyanis e háromszögek $\rho $-val szemben fekvő szögei fele akkorák, mint az eredeti háromszög hegyes szögei, tehát kisebbek 45\r{ }-nál. Eszerint $x,\mbox{ }y\mbox{ }\rangle \mbox{ }\rho =3$, így $x-3,\mbox{ }y-3$ pozitívok és $a\mbox{ }\langle \mbox{ }b$-re tekintettel $x-3\mbox{ }\langle \mbox{ }y-3$. Így 18-nak ismét csak a pozitív tényezőkre való felbontásai jönnek szóba:

$ \begin{array}{l} a=x+3=\left( {x-3} \right)+6\mbox{ = 7, 8, 9,} \\ b=y+3=\left( {y-3} \right)+6\mbox{ =24, 15, 12,} \\ c=x+y=\left( {x-3} \right)+\left( {y-3} \right)+6=25\mbox{, 17, 15,} \\ \end{array} $

ismét az 1. megoldásban nyert háromszögekre jutottunk. Megjegyzés: A kitűzött feladat speciális esete a következő feladatnak: Egy derékszögű háromszög oldalainak mértékszámai egész számok. A háromszög területe mértékszámának $\rho $ {\-}szorosával, ahol $\rho $ adott pozitív egész szám. Mekkorák a háromszög oldalai? (Esetünkben $\rho $ =3 volt.) A követelmény szerint a $ 2t\mbox{ : }2s$ arány értéke $\rho $, az ezzel egyenlő $t $: $s$ arány viszont - mint láttuk - a beírt kör sugarát adja meg, ennélfogva a $\rho $ szám minden megoldásban a beírt kör sugarának mértékszáma. Ebből a 2. megoldás gondolatmenetével (4) helyett az

diofantoszi egyenletre jutunk. Ebből annyi megoldást nyerünk, ahányféleképpen $ 2\rho ^2$-et két pozitív egész tényező szorzatára lehet bontani, ugyanis $\rho ,\mbox{ }x-\rho ,\mbox{ }y-\rho $-val együtt $x$, $y \quad a=x+\rho $, $b=y+\rho $ és $c=x+y$ szintén egész számok. Érdekes, hogy $\rho $ minden értéke mellett van olyan megoldás, melyben az oldalak aránya 3~:~4~:~5. Erre vezet ugyanis $ 2\rho ^2$-nek $\rho \cdot 2\rho $ alakú felbontása: $x-\rho =\rho $, $y-\rho =2\rho $-ból $x=2\rho $, $y=3\rho $ és $a=3\rho $, $b=4\rho $, $c=5\rho $.

3. Megoldás

Ismeretes, hogy az (1) pitagoraszi egyenletet kielégítő $a$, $b$, $c$ egész számhármasokat pitagoraszi számhármasoknak szokás nevezni. Az ilyeneknek minden$\lambda a,\mbox{ }\lambda b,\mbox{ }\lambda c$ többszöröse - ha $\lambda $ pozitív egész szám - ugyancsak pitagoraszi számhármas. Ha $a$ és $b$ relatív prímek, akkor $c$ és $a$, továbbá $c$ és $b$ szintén relatív prímek, ilyen esetben $a$, $b$, $c$-t alaphármasnak nevezzük. Ismeretes az is, hogy minden alaphármas kifejezhető két $u$, $v$ paraméterrel a következőképpen:

ahol $u$ és $v$ pozitív egész, páratlan relatív prím számok. Ezekkel minden pitagoraszi számhármas így írható:

ugyanis minden pitagoraszi számhármas valamely alaphármas többszöröse. Feladatunk most már a közül kiválasztani a (2)-nek eleget tevő számhármasokat. (Az $a<b$követelményt a továbbiakban természetesen nem tarthatjuk fenn, mert $a$ és $b$ kifejezése lényegesen különböző.) E kifejezéseket (2)-be beírva $b+c=\lambda u^2$ alapján a

egyenletre jutunk. Ezt $\lambda $-val, $u$-val és $u+v$-vel oszthatjuk, mert egyikük sem 0:

A bal oldal tényezői közül $v$ páratlan, $u-v$ páros, és $\lambda $ tetszőleges pozitív egész. Másrészt$ 6=2\cdot 3=1\cdot 2\cdot 3$, így a tényezők megfeleltetésére a következő lehetőségek vannak:

678

ekkor $\lambda =\mbox{ }3,\mbox{ }1,\mbox{ }1,$ és $u=\mbox{ }3,\mbox{ }7,\mbox{ }5,$ ennélfogva szerint

Ismét az előzők során nyert háromszögekhez jutottunk. Látjuk továbbá a $\lambda =1$értékből, hogy a második és a harmadik megoldás alaphármas. Valóban, a 7, 24, 25 és a 15, 8, 17 számok páronként relatív prímek, az első hármas viszont $\lambda =3$-szorosa a 3, 4, 5 alaphármasnak.