Bizonyítsuk be, hogy ha két hatszög oldalainak felezőpontjai rendre megegyeznek, akkor a két hatszög területe egyenlő.

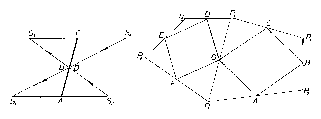
Legyen a $P_1 P_2 P_3 P_4 P_5 P_6 =P$ hatszög $P_1 P_2 ,\mbox{ }P_2 P_3 ,\mbox{ ..., }P_6 P_1 $ oldalának felezőpontja rendre $A$, $B$, $C$, $D$, $E$, $F$, és tegyük fel, hogy rendre ugyanezen pontok felezik a $Q_1 Q_2 Q_3 Q_4 Q_5 Q_6 =Q$ hatszög egymás utáni $Q_1 Q_2 ,\mbox{ }Q_2 Q_3 ,\mbox{ ..., }Q_6 Q_1 $ oldalát is. Azt kell bebizonyítanunk, hogy a $P$ és $Q$ hatszögek területe egyenlő. Egyelőre feltesszük, hogy sem $P$, sem $Q$ nem hurkolt idom és meggondolásainkat az 1. ábra esetéhez kapcsoljuk hozzá. A közös felezőpontokban a két hatszög egy-egy oldallal metszi egymást, pl. $A$-ban a $P_1 P_2 $ és $Q_1 Q_2 $ oldalak. Ezért az egyik hatszög kerületén végighaladva mindegyik felezőpontban átlépjük a másik hatszög kerületét, vagy belépünk abba, vagy kilépünk belőle, - hacsaknem kivételesen $P$ és $Q$ egy-egy oldalegyenese egybeesik, és így egy szakaszon közös határon haladunk. Ennél fogva $Q$ területének is bizonyos részei $P$-n kívül és viszont. Pl. az $AP_1 Q_1 $ háromszög $P$-hez hozzátartozik, $Q$-hoz pedig kívülről csatlakozik, az $AP_2 Q_2 $ háromszög viszont $Q$-n belül egyszersmind $P$-n kívül van. E két háromszög egybevágó, mert $A$-ból kiinduló oldalaik páronként egyenlők és a köztük levő szögek csúcsszögek, ezért területük is egyenlő. Így kapjuk a következő 6 egyenlőséget (a háromszögek területét ugyanúgy jelölve, ahogy magukat a háromszögeket szokás):

A balról felsorolt háromszögek mind kívülről csatlakoznak $Q$-hoz, a jobboldaliak pedig $P$-hez. Ezért $Q$-hoz hozzávéve a bal oldali háromszögeket, az $AQ_2 BP_3 CQ_4 P_4 DQ_5 EP_6 Q_6 FP_1 =S$ sokszöget kapjuk. Ugyanezt a sokszöget kapjuk $P$-ből a jobb oldalon felsorolt háromszögek hozzátételével. Eszerint a $P$, $Q$, $S$ idom területét is $P$-vel, $Q$-val, ill. $S$-sel jelölve, a egyenlőségek összeadásával adódó egyenlőség két oldalának értékét pedig $T$-vel, a következő egyenlőséget írhatjuk fel:

Innen $Q=P$. Ezzel az állítást - az ábrán felvett esetre - bebizonyítottuk.

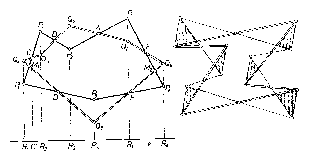
Megjegyzés: Számos versenyző a $P $és $Q$ hatszögek közös részéhez,a $Q_1 AP_2 BQ_3CM_1DP_5 EM_2 F$ sokszöghöz vette hozzá a bal-, ill. jobboldalon álló háromszögeket. ($M_1 $ a $P_3 P_4 $ és $Q_4 Q_5 $, $M_2 $ pedig a $P_6 P_1 $ és $Q_5 Q_6 $ oldalak közös pntja, ezek nem egymásnak megfelelő oldalak, csak esetleges, hogy van közös pontjuk, ábránkon több ilyen oldalpár nincs is.) Egy részük nem vette észre, hogy így nem $P$-t, ill. $Q$-t kapta, hanem nagyobb idomot, mert egy-egy hozzávett háromszög részei, az $M_1 P_4 Q_4 $ és $M_2 P_6 Q_6 $ háromszögek sem $P$-hez, sem $Q$-hoz nem tartoznak hozzá. Mások ezek elvételével tették teljessé bizonyításukat. A háromszögekkel ,,kétszer fedett'' $M_1 P_4 Q_4 $ háromszög azért keletkezett, mert a $C$, $D$ egymás utáni felezőpontok a $P_4 Q_4 $ egyenes ugyanazon oldalán vannak. Ha egy ilyen $P_i Q_i $ egyenes átmegy a $P_{i-1} P_i $, vagy a $P_i P_{i+1} $ oldal felezőpontján, akkor felsorolás megfelelő háromszöge egyenes szakasszá fajul, egyszersmind kétszer fedett háromszög sem keletkezik. Előfordulhat viszont, hogy mind a hat$P_i Q_i $ szakaszon létrejön kétszer fedett háromszög.

2. Megoldás

$P$ és $Q$ egy-egy közös felezőponttal bíró oldalának - pl. az egymást $A$-ban felező$P_1 P_2 $, $Q_1 Q_2 $ oldalpárnak - végpontjai paralelogrammát alkotnak, ezért $P_1Q_1 \left\| {Q_2 P_2 \left\| {P_3 Q_3 \left\| {Q_4 P_4 \left\| {P_5 Q_5 \left\| {Q_6 P_6 } \right.} \right.} \right.} \right.} \right.$. Vegyünk egy a $P_1 Q_1 $-re merőleges, sem $P$-t, sem $Q$-t nem metsző $e$ egyenest, és vetítsük erre $P$ és $Q$ csúcsait. A $P_1 ,\mbox{ }Q_1 ,$ a $P_2 ,\mbox{ }Q_2 ,$ ..., a $P_6 ,\mbox{ }Q_6 $ pontpárok vetülete egybeesik, jelöljük ezeket rendre $R_1 ,\mbox{ }R_2 ,\mbox{ ..., }R_6 $-tal (1. ábra, ezek közül egyesek egybe is eshetnek). Ekkor $P$ és $Q$ területét úgy kaphatjuk, hogy 4-4 trapéz területének összegéből kivonjuk más 2-2 trapéz területének összegét:

A két kifejezés ugyanazon sorszámú tagjai páronként egyenlők, mert a megfelelő trapézek magassága és középvonala közös, pl. az első tagokra$R_4 R_3 $ és CC', ahol $C'$ a $C$-nek $e$-n levő vetülete. Ezért $P = Q$. Az ábránkétól különböző esetekben a előállításokban a hozzáadandó tagok száma legalább 1, legfeljebb 5, és ezt a számot a levonandó tagok száma 6-ra egészíti ki. Amennyiben szomszédos indexű $R$ pontok egybeesnek, a tagok száma csökken. Megjegyzések: 1. A most bemutatott módon szokás meghatározni sokszögek területét, ha csúcsaik koordinátáikkal vannak adva. Így határozza meg a földmérő mérnök is sokszög alakú telkek területét. 2. Ez a bizonyítás mutatja, hogy az állítás az 1. ábra esetében is érvényes, ahol $P$ és $Q$ közös része nem összefüggő: két négyszögre és egy hatszögre esik szét. Ebben az esetben az 1. megoldás megjegyzésében említett meggondolást jelentősen ki kellene egészítenünk.

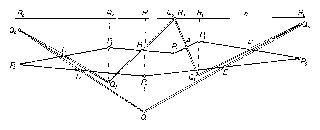
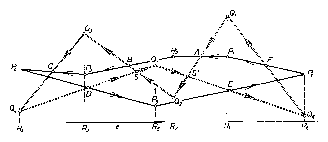
3. A 2. ábra esetében $Q$ hurkolt, $Q_2 Q_3 $ és $Q_4 Q_5 $ oldalszakaszainak közös pontja $S$, a $Q_1 Q_2 $ és $Q_5 Q_6 $ szakaszok közös pontja $S'$. Ilyen idom területét eddig nem értelmeztük. Az oldalszakaszok, ill. részeik $Q_1 S'Q_6 =H_1 $ és $SQ_3 Q_4 =H_2 $ háromszögeket és az $S'_1 Q_2 SQ_5 =N$ négyszöget határolják körül. Nézzük meg, mit ad ebben az esetben a 2. megoldás gondolatmenete. $N$ területét pozitív tagjaiban nem vettük számításba, mert a négyszög az $R_3 Q_3 Q_2 R_2 $, $R_2 Q_2 Q_1 R_1 $ trapézeken kívül van, a negatív tagokban viszont levontuk, mert az $R_4 Q_4 Q_5 R_5 ,\mbox{ }R_5 Q_5 Q_6 R_6 $ trapézok tartalmazzák. Eszerint az állítás érvényes marad, ha $Q$ területén ezúttal a $H_1 +H_2 -N$ kifejezést értjük. (Könnyen megjegyezhető ez a megállapodás, ha összehasonlítjuk a $H_1 ,\mbox{ }H_2 $ és $N$ részek körüljárásának irányát, miközben $Q$ kerületét $Q_1 ,\mbox{ }Q_2 ,\mbox{ }Q_3 ,\mbox{ }Q_4 ,\mbox{ }Q_5 ,\mbox{ }Q_6 $ sorrendben körüljárjuk. $H_1 $ és $H_2 $ körüljárása az óramutató járásával ellentétes irányú, akárcsak a $P=P_1 P_2 P_3 P_4 P_5 P_6 $ körüljárásé, $N$ körüljárása pedig az óra járásával megegyező. Másképpen: $H_1 ,\mbox{ }H_2 $ és $P$ körülhatárolt része a mondott körüljárásban a menetvonal bal oldalán van, $N$-é pedig a jobb oldalon.)

3. Megoldás

Ismeretes, hogy bármely négyszög oldalfelező pontjai egy paralelogramma csúcsai, melynek oldalai párhuzamosak a négyszög átlóival és fele akkorák, mint az átlók (1. ábra, $P_1 P_2 P_3 P_4 $ és ABCG). Megmutatjuk, hogy a paralelogramma területe fele a $P_1 P_2 P_3 P_4 $ négyszög területének. Valóban, a $P_2 P_4 $ átló $H$ felezőpontját $A$-val, $B$-vel, $C$-vel, ill. $G$-vel összekötő szakasz rendre párhuzamos és egyenlő a $P_4 P_1 ,\mbox{ }P_4 P_3 ,\mbox{ }P_2 P_3 ,$ ill. $P_2 P_1 $ oldal felezésével előállt szakaszokkal. Ezért az ABH és CGH háromszögek áttolhatók $GCP_4 $-be, ill. $BAP_2 $-be és a BCH és GAH háromszögek 180\r{ }-os forgatással átforgathatók $CBP_3 $-ba, ill. $AGP_1 $-be. Így pedig a négy részre darabolt ABCG paralelogramma részeivel maradéktalanul lefedhetjük a $P_1 P_2 P_3 P_4 $ négyszögnek a paralelogrammán kívüli részeit.

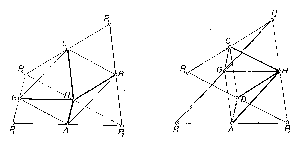
(Állításunk hurkolt négyszögre is igaz, ha ennek területét a fenti megjegyzés szerint értelmezzük, továbbá a felhasznált háromszögek területét pozitív, ill. negatív előjellel tekintjük aszerint, hogy felsorolt körüljárásuk iránya megegyező, ill. ellentétes az ABCG paralelogramma körüljárásának irányával. Ha a hurkolt négyszöget az $S_1 S_2 S_3 S_4 $ paralelogrammából képezzük az $S_2 $ és $S_4 $ csúcsok felcserélésével, akkor az oldalfelező pontok egy egyenesre esnek (2. ábra), $ABCD=0$, megfelelően annak, hogy $S_1 S_2 B\Delta \cong S_4 S_3 D\Delta $, és így különbségük 0. A továbbiakban is minden területet így értünk.)

Ezek szerint a fenti $P$ hatszöget a $P_1 P_4 $ átlóval a $P_1 P_2 P_3 P_4 $ és $P_1 P_4 P_5 P_6 $ négyszögekre bontva és ezen átló felezőpontján $G$-vel jelölve $P$ területe kétszerese az ABCG és GDEF paralelogrammák területe összegének. Ha mármost $Q$ hatszög oldalainak felező pontjai ugyancsak rendre az $A$, $B$, ..., $F$ pontok, akkor $Q$ területe is kétszerese a paralelogrammák negyedik ($G)$ csúcsát az első három csúcs egyértelműen meghatározza, ha sorrendjük is adva van. Ezzel az állítást bebizonyítottuk.

Megjegyzések:

1. Látható, hogy a négyszögoldalak felezőpontjai közül csak 3 független egymástól $A$, $B$, $C$ és sorrendjük - meghatározza $G$-t. Másrészt az is, hogy tetszés szerinti számú olyan négyszög szerkeszthető, melyre az oldalak felezőpontjai rendre azonosak $A$, $B$, $C$, $G$-vel. Ha ugyanis egy tetszés szerinti$S_1 $ pont $A$-ra vett tükörképe$S_2 $, $S_2 $-é $B$-re $S_3 $ és $S_3 ${\-}é $C$-re $S_4 $, akkor $S_4 $-nek $G$-re vett tükörképe azonos $S_1 $-gyel. Hasonlóan a hatszögoldalak felezőpontjai közül csak öt független egymástól. Pl. felvéve az $A$, $B$, $C$, $D$ és $E$ pontokat, megszerkeszthetjük a $G$ pontot, mint az ABCG paralelogramma negyedik csúcsát, majd az $F$ pontot, mint a GDEF paralelogramma negyedik csúcsát. Ha viszont az adott 6 felezőpont megfelel e feltételnek, akkor az előbbihez hasonló tükrözéssorozattal akárhány olyan hatszög szerkeszthető, melyre az egymás utáni oldalak felezőpontja $A$, $B$, $C$, $D$, $E$, $F$.

2. Az eddigi felezőpontokat $A$, $B$, $C$, $F$, $E$, $D$ sorrendben véve a létrejövő hatszögek területe az előbbiekétől különböző, mert így a DEFG paralelogramma helyére FEDG lép, és ezek területei egymásnak negatívjai. Ezért nem felesleges a feladatnak az a kikötése, hogy a hatszögoldalak felezőpontjainak rendre kell megegyezniük.

3. Az állítás hatszög helyett bármely páros oldalszámú sokszög esetére érvényes, megjegyezve azt, hogy az utolsó felezőpontot a többiek - és sorrendjük - egyértelműen meghatározzák. Ez abból következik, hogy minden $ 2n$ oldalú sokszög $\left( {2n\ge 6} \right)$ egy csúcsból kiinduló átlókkal $n-1$ négyszögre bontható. Néhány versenyző akárhány oldalú sokszögre érvényesnek vélte az állítást. Ez a sejtés a páratlan oldalszámú sokszögre semmitmondó. Ugyanis egy háromszög oldalainak felezőpontjai egyértelműen meghatározzák a háromszöget, és ugyanez áll a $ 2n-1$ oldalú szögekre $\left( {2n-1\ge 5} \right)$, mert ezekben egy csúcsból azokat az átlókat meghúzva, amelyek a sokszöget egy négyszögre és egy $ 2n-3$, ill. $ 2n-5$, ...- szögre bontják (pl.) $P_1 P_4 ,\mbox{ } \quad P_1 P_6 , \quad P_1 P_8 ,$ $\mbox{..., }P_1 P_{2n-2} )$ utoljára háromszöget kapunk. Ezt az oldalak felezőpontjai egyértelműen meghatározzák és ebből kiindulva a sokszög többi csúcsai is egyértelműen meghatározhatók.