Az ABC hegyesszögű háromszög oldalfelező pontjaiból merőlegeseket állítunk a szomszédos oldalakra. Ezeknek a merőlegeseknek a háromszögön belüli metszéspontjai és a háromszög oldalfelező pontjai egy hatszöget határoznak meg. Hányad része a hatszög területe a háromszög területének?

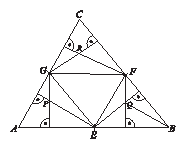
Legyenek a háromszög oldalfelezési pontjai az ábrának megfelelően $E; F; G;$ e pontokból húzott merőlegesek metszéspontjai $P; Q; R$. Jelöljük az ABC területét t-vel. Kössük össze a $G; E; F$ pontokat, így az ABC középvonalait kapjuk, amelyek négy egybevágó háromszögre bontják az ABC$\Delta $-et.

Az EBF$\Delta \cong $GFC$\Delta \cong $AEG$\Delta $, így területük $\frac{t}{4}$. A $Q$ pont az EBF magasságpontja, mert a háromszög két magasságvonalának metszéspontja. Ugyanezért a $P$ az AEG$\Delta $, az $R$ a GFC$\Delta $ magasságpontja. A magasságpontokat a háromszög csúcsaival összekötve egybevágó részháromszögeket kapunk. Ezért FBQ$\Delta \cong $GEP$\Delta $, és EBQ$\Delta \cong $GFR$\Delta $. Ezek után a keresett terület: