Adva vannak valamely ABCD derékszögű négyszög AB és CD, valamint AD és BC oldalainak $M$ és $N$, illetőleg $P$ és $Q$ metszéspontjai egy $e$ egyenessel, továbbá AB oldalának $p$ hossza; szerkesszük meg a derékszögű négyszöget. Mikor oldható meg a feladat, és hány megoldása van?

PQ fölött mint átfogó fölött olyan PSQ derékszögű háromszöget szerkesztünk, amelyben PS = p ( 1. ábra). Az $M$ és $N $pontokon keresztül PS-l párhuzamos egyeneseket vonva, ezek és a $P$-n meg Q-n keresztül reájuk merőlegesen vont egyenesek a feladatnak megfelelő derékszögű négyszöget adnak. A feladat csak akkor oldható meg, ha a PSQ háromszög valóban megszerkeszthető, azaz ha $p <$ PQ.

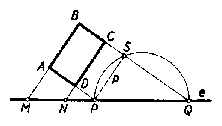
Ha ez a feltétel teljesül, akkor a PSQ háromszöget az $e$ egyenesnek két különböző oldalán rajzolhatjuk, tehát két megoldást kapunk, amelyek $e$-re vonatkozólag egymásnak tükörképei.