(Feladat azonosítója: VF_000828 )
Témakör: *Geometria
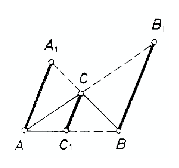
Az ABC háromszög AB oldalán $A$ és $B$ között választott $C$; pontot kössük össze $C$-vel. Az $A$ szögponton áthaladó és CC$_{1}$-gyel párhuzamos egyenes messe BC-t az $A_{1}$ pontban, a $B $szögponton áthaladó és CC$_{1}$-gyel párhuzamos egyenes messe AC-t a $B_{1}$ pontban.
Bizonyítsuk be, hogy
$ \frac{1}{AA_1 }+\frac{1}{BB_1 }=\frac{1}{CC_1 }. $
Minthogy AA$_{1}$, BB$_{1}$ és CC$_{1}$ egymással párhuzamos egyenesek (ábra), azért
CAC$_{1}$$\Delta \quad \sim $ B$_{1}$AB$\Delta $ és CBC$_{1}$$\Delta \quad \sim $ A$_{1}$BA$\Delta $.
Az innen következő
CC$_{1} : B_{1}$B = AC$_{1}$ : AB,
CC$_{1} : A_{1}A = C_{1}$B : AB
aránypárokból
$ \frac{CC_1 }{A_1 A}+\frac{CC_1 }{B_1 B}=\frac{AC_1 +C_1 B}{AB}=\frac{AB}{AB}=1. $
Tehát
$ \frac{1}{A_1 A}+\frac{1}{B_1 B}=\frac{1}{CC_1 }. $