Adva van a térben négy pont: $A$, $B$, $C$, $D$. Meghatározandó az $S$ sík úgy, hogy $A$ és $C$ a sík egyik oldalán, $B$ és $D$ a sík másik oldalán legyen, és hogy a négy pont $S$-től egyenlő távolságra legyen.

Az $S$ sík úgy határozandó meg (1. ábra), hogy $A$-nak és $B$-nek. $B$-nek és $C$-nek. $C$-nek és $D$-nek végre $D$-nek és $A$-nak $S$-től való távolsága egyenlő nagy, de ellenkező irányú legyen. Az első három követelés teljesüléséből már következik, hogy teljesül a negyedik is.

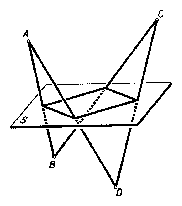
Egy sík két oldalán egy-egy pont akkor és csak akkor van a síktól egyenlő távolságra, ha a sík felezi a két pont összekötő távolságát. Az első három követelés tehát akkor és csak akkor teljesül, ha az $S$ sík áthalad az AB, BC, CD szakaszok felezőpontján. Feladatunk megoldását tehát e három felezőpont síkja adja. Ha a felezőpontok egy egyenesen vannak, akkor az adott 4 pont egy síkban van, mert AC és BD is párhuzamos a felezőpontokon átmenő egyenessel, s így $D $benne van az $A, B, C$ pontokat tartalmazó síkban. Ha az egyik adott pont rajta van azon az egyenesen, ami átmegy a felezőpontokon, akkor a többi három is rajta van. Ez esetben nem létezik a feltételeknek megfelelő sík. Ha a négy pont egy síkban van, de nem egy egyenesen, akkor a felező pontok egyenesén átmenő minden sík megfelel a követelményeknek, kivéve az adott pontokat tartalmazó síkot.