Adva van a síkban három egy ponton átmenő és páronként $ 60^\circ $-os szöget bezáró egyenes: $p$, $q$ és $r$, továbbá három hosszúság: $a\le b\le c$. Bizonyítsuk be, hogy azok a pontok, amelyeknek az adott egyenesektől való távolsága rendre kisebb $a$, $b$, illetve $c$-nél, akkor és csak akkor alkotják egy hatszög belsejét, ha a+b $>$ c. Ha a feltétel ki van elégítve, mekkora a hatszög kerülete?

Azok a pontok, amelyeknek $p$-től való távolsága $a$-nál kisebb, a $p$ középvonalú, $ 2a $szélességű sáv belsejét alkotják (1. ábra)$. $Feladatunk tehát a $p, q , r$ középvonalú és rendre 2a, 2b, 2c szélességű sávok közös részéről szól. E sávok mindegyike szimmetrikus a $p, q, r$ egyenesek közös $O$ pontjára nézve. Ezért közös részük is szimmetrikus $O$-ra, tehát páros oldalszámú sokszög. Annak feltételét kell keresnünk, hogy e közös rész mikor nem négyszög, azaz mikor nem azonos két sáv közös részével. Tekintsük először csak a $p$ és $q$ középvonalú sávokat. Ezeknek közös része paralelogramma. Megvizsgáljuk, hogy ennek a paralelogrammának pontjai $r$-től mekkora távolságra vannak. Eljuthatunk az $O$ pontból ennek a paralelogrammának bármely belső pontjához úgy, hogy először $p$-vel párhuzamosan , majd $q$-val párhuzamosan haladunk. A$ p$-vel párhuzamos elmozdulásnak $q$-ra merőleges összetevője $b$-nél kisebb, és mindkét irányban minden $b$-nél kisebb értéket felvehet.

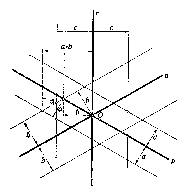
Minthogy egyeneseink 60\r{ }-os hajlása miatt $q$ és $r$ szimmetrikusan helyezkednek el a $p$ egyenesre nézve, az említett elmozdulásnak $r$-re merőleges összetevője ugyanakkora, mint a $q$-ra merőleges összetevő; tehát ez is kisebb $b$-nél, és mindkét irányban minden $b$-nél kisebb értéket felvehet. Ugyanígy látható be az is, hogy amikor $O$-ból két elmozdulással a paralelogramma valamely belső pontjához jutunk, akkor a második, $q$-val párhuzamos elmozdulásnak $r$-re merőleges összetevője $a$-nál kisebb, és mindkét irányban minden $a$-nál kisebb értéket felvehet. A két elmozdulás egymásutánját tekintve elmondhatjuk tehát, hogy paralelogrammánknak belső pontjai $r$-től $a+b$-nél kisebb távolságra vannak, és mindkét irányban minden $a+b$-nél kisebb távolságra van a paralelogrammának pontja. Megállapításainkból következik, hogy a tekintett paralelogramma akkor nem közös része mindhárom sávnak, ha $a+b>c$. Ha a $p$ és $q$ középvonalú sávok helyett másik két sáv alkotta paralelogrammát tekintünk, akkor ugyanolyan megfontolással következik, hogy ezek akkor nem közös részei mindhárom sávnak, ha $b+c>a$ és $a+c>b$. Ez a két feltétel azonban $a\le b\le c$ miatt mindig teljesül. Az $a+b>c$ feltétel tehát szükséges, és önmagában elegendő ahhoz, hogy a feladatban jellemzett pontok hatszöget alkossanak. A hatszög kerületének meghatározásához megmutatjuk, hogy a $p, q, r$ egyenesek alkotta 60$^{0}$ -os szögtartományokba kerülő rész egyenlő azzal a szakasszal, amelyet a szögtartományt alkotó szárak a harmadik egyenessel párhuzamos sáv határvonalából kimetszenek. Vegyünk egy 60\r{ } -os szögtartományt és a harmadik egyenessel párhuzamos sávnak a szögtartományba eső részét (2. ábra). Ha ez teljesen a hatszöghöz tartozik, akkor állításunk magától értetődő. Ha viszont e tartomány valamelyik része egy másik sávon kívül esik, akkor e kieső rész szabályos háromszög, s így a két sáv határának ezt határoló szakaszai (az ábrán egyenlően jelölt szakaszok) egyenlők. Állításunk tehát ebben az esetben is helyes.

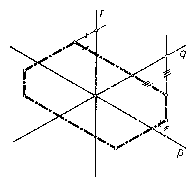
Ezek szerint a hatszög kerülete akkora, mint a két-két $a,b$ illetőleg $c$ magasságú szabályos háromszög oldalának összege, azaz