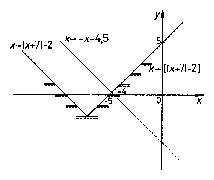Oldjuk meg a

egyenletet ($\left[ a \right]$ jelöli $a$ legnagyobb, $a$-nál nem nagyobb egész számot)!

A négyzetgyökjel alatt az $\left( {x+7} \right)^2$ áll, ezért egyenletünk az

egyenlettel ekvivalens. Vizsgáljuk először az $x+7\ge 0$ esetet. Ekkor bal oldala $\left[ {x+5} \right]$-vel egyenlő. A két oldal közös értékét $k$-val jelölve, $k$ nyilvánvalóan egész szám és $k=-x-4,5$-ből $x=-k-4,5$, amelyet -be helyettesítve:

Mivel $-k<0,5-k<1-k$, ezért utóbbi egyenletünk bal oldala --$k$-val egyenlő, ahonnan $-k=k$, $k=0$, tehát $x=-4,5$. Ez valóban megoldása az egyenletnek. Ha most $x+7<0$, akkor bal oldala $\left[ {-x-9} \right]$. A két oldal közös értékét jelölje most is $k$. A $k$ egész szám és a $k=-x-4,5$-ből $x=-k-4,5$, amivel a

alakot ölti. A $k-5<k-4,5<k-4$ miatt $\left[ {k-4,5} \right]=k-5$, ezért utóbbi egyenletünknek nincs megoldása, ennélfogva az $x=4,5$ az eredeti egyenlet egyetlen megoldása.

2. Megoldás

Az egészrész értelmezéséből ($a-1<\left[ a \right]\le a)$:

Az $x+7\ge 0$ esetben ez az egyenlőtlenséglánc ekvivalens

egyenlőtlenséglánccal. Ennek bal oldalából $ 2x<-8,5$, azaz $x<-4,25$; jobb oldalából pedig $-9,5\le 2x$, azaz $-4,75\le x$. Az eredeti egyenlet bal oldala egész szám, tehát jobb oldala, a $-x-4,5$ is egész. A $-4,75\le x<-4,25$ feltétel miatt egyedül az $x=-4,5$ felelhet meg. Ez valóban megoldás. Ha $x+7<0$, akkor -ből

azaz $\left( {x+4,5} \right)$-et adva mindhárom számhoz, a

ellentmondásra jutunk.

3. Megoldás

Egyenletünk bal oldalán álló $\left[ {\left| {x+7} \right|-2} \right]$ kifejezést ábrázoljuk a jobb oldali $-x-4,5$ kifejezéssel együtt, egy derékszögű koordináta-rendszerben (1. ábra). A két grafikonnak egyetlen közös pontja van, leolvasásunk szerint az $x=-4,5$ abszcisszájú pontban. Ez valóban megoldás.