Egy $O$ középpontú kör kerületén mozog egy $P$, melynek vetülete a rögzített AB átmérőn $P$'. Az OP sugárra mérjük fel $O$-tól az $OQ=PP'$ szakaszt! Milyen alakzatot alkotnak a $Q$ pontok, ha $P$ végigfut a körön?

Legyen az AB-re merőleges átmérő a CD. A kör szimmetrikus ezekre az átmérőkre, és a kör középpontjára is, ennélfogva a keresett alakzat is szimmetrikus mind az átmérőkre, mind a kör $O$ középpontjára. Elég tehát a BC negyedkörív $P$ pontját vizsgálni (1.~ábra).

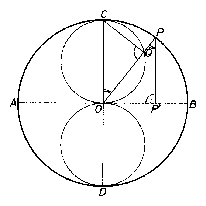
Legyen a $P$ a BC ív egy tetszőleges belső pontja! Az OPP' és az OCQ háromszögek egybevágók, hiszen $OP=OC$, $PP'=OQ$ és $COQ\angle =OPP'\angle $, mert váltószögek. Következésképpen $OQC\angle =90^{\circ}$, tehát $Q$ rajta van az OC Thalész-körének az OCB negyedkörébe eső ívén. $O$ és $C$ pontjai a keresett alakzatnak, hiszen ha $P=B$, illetve $P=C$, akkor a $Q$ pont éppen $O$, illetve $C$. Az említett félkörív minden belső $Q$ pontjához található a BC negyedköríven oly $P$ pont, amelynek $P$' vetületére a $PP'=OQ$ teljesül. Ugyanis az OQ félegyenesnek a körrel való $P$ metszéspontja ilyen tulajdonságú, hiszen $OCQ\Delta \cong OPP'\Delta $, mert $OC=OP$, mindkét háromszög derékszögű és $COQ\angle =OPP'\angle $, mert váltószögek. Ebből $OQ=PP'$ következik. Ezzel beláttuk, hogy a keresett alakzat két, mégpedig az OC és az OD átmérőjű kör.

2. Megoldás

Az AB átmérőre vonatkozó szimmetria miatt elég azzal az esettel foglalkozni, amikor $P$ az ACB félkört futja be. A $C$ pontra illeszkedő, esetleg elfajuló CC' húrok $Q$ felezőpontjainak mértani helye a CO szakasz Thalész-köre, hiszen a $C$ közepű $ 1 2$ arányú hasonlósági transzformáció a $C$' pontokat a CC' húrok felezőpontjába, az $O$ közepű OA sugarú kört az OC Thalész-körébe viszi.

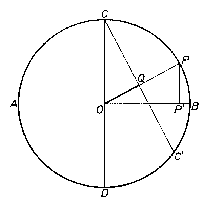
Azt fogjuk tehát bizonyítani, hogy $OQ=PP'$ és az ACB félkör bármely $C$-től különböző $P$ pontjának az OC Thalész-körével való közös $Q$ pontja egy $C$ végpontú, $Q$-ra illeszkedő CC' húr felezőpontja. Ez utóbbi Thalész tétele miatt nyilvánvaló, mivel OQ merőleges CC'-re, ezért felezi is azt. Ugyanezért $OCQ\Delta \cong OPP'\Delta $, mert mindkettő derékszögű, $OCQ\angle =POP'\angle $ merőleges szárú hegyesszögek lévén, és $C=OP$, tehát $OQ=PP'$! A $C=C'$-re $OQ=PP'$ nyilvánvaló. Ezzel beláttuk, hogy $Q$ pontok halmaza két, az AB-re szimmetrikus, OC, illetve OD átmérőjű kör.