(Feladat azonosítója: VF_000146 )
Témakör: *Algebra (egyenlőtlenség)
Bizonyítsuk be, hogy minden $x\ge 1 2$ valós számra
$ \sqrt {9x+7} <\sqrt x +\sqrt {x+1} +\sqrt {x+2} <\sqrt {9x+9} ! $
A jobb oldali egyenlőtlenség azonnal adódik abból, hogy a négyzetgyök-függvény alulról konkáv, vagyis a függvénygörbe bármely két pontját összekötő ív az e pontokhoz tartozó húr felett van (1. ábra). Emiatt ugyanis:
$ \sqrt x +\sqrt {x+2} <2\sqrt {x+1} , $
és innen
$ \sqrt x +\sqrt {x+1} +\sqrt {x+2} <3\sqrt {x+1} =\sqrt {9x+9} $
következik.
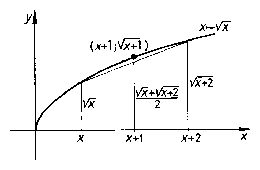
Minthogy $\sqrt {x+7 9} <\sqrt {x+1} $, ezért az eredeti egyenlőtlenséglánc bal oldalának igazolásához elég azt megmutatni, hogy
$ \left( {0\le } \right)2\sqrt {x+\frac{7}{9}} <\sqrt x +\sqrt {x+2} . $
Négyzetre emeléssel
$ 4x+\frac{28}{9}<2x+2+2\sqrt {x^2+2x} , $
majd rendezéssel
$ 0<x+\frac{5}{9}<\sqrt {x^2+2x} $
adódik. Újból négyzetre emelve, átrendezve
$ \frac{25}{81}<2x-\frac{10x}{9}, $
azaz $x>\frac {25} {72}$ adódik. A bal oldali egyenlőtlenség tehát igaz, mivel a feltétel szerint $x\ge 1 2$, továbbá átalakításaink emiatt megfordíthatóak voltak.