Egy adott rombusz oldalait érintő kör sugara $R$. Az $R$ sugarú kört és a rombusz két oldalát érintő kör sugara pedig $r$. Mekkora a rombusz átlói hosszának aránya, ha $r/R=1/4$?

Legyen $AB=BC=CD=DA=a$; $AC=f$ és $BD=e$ hosszúságú. A rombusz átlói merőlegesek egymásra. $AO_1 D\Delta \sim O_1 T_1 D\Delta $ mert derékszögűek és $T_1 DO_1 $ szögük közös. Ebből következik, hogy megfelelő oldalak aránya megegyezik:

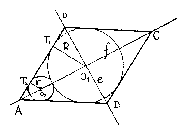
$AO_2 T_2 \Delta $ és $AO_1 T_1 \Delta $ középpontos ($A$-ra) hasonlósága miatt:$r/R=\overline {AO_2 } /\overline {AO_1 } $ Mivel $\overline {AO_2 } =\frac{f}{2}-\left( {r+R} \right)$ és $\overline {AO_1 } =\frac{f}{2}$

(1.)-ből $a=\frac{e\cdot f}{4R}$ (1'.) (2.)-ból $f=\frac{8}{3}\left( {r+R} \right)$ (2'.) (1'.) és (2'.) egybevetéséből és a $r/R=1/4$ feltételéből $a=\frac{5}{6}e$ következik (3.) Mivel $AO_1 D\Delta $-re Püthagorasz tételéből $a^2=\frac{e^2}{4}+\frac{f^2}{4}$ adódik. (3.) felhasználásával: $\frac{25}{36}e^2=\frac{e{ }^2}{4}+\frac{f^2}{4}$ ahonnan összevonás és $f^{2}$-tel való osztás után:$\frac{e^2}{f^2}=\frac{9}{16}$ amiből ( $\frac{e}{f}\rangle 0$ miatt) a keresett arány: $e$ : $f$ = 3 : 4.