Vegyes feladatok: VF_000203
(Feladat azonosítója: VF_000203 )
Témakör: *Kombinatorika

Hányféleképpen helyezhető el két azonos színű (egyforma) futó a 8$\times $ 8-as sakktáblán úgy, hogy ne üssék egymást (azaz ne legyenek egy átlós irányú egyenesen)?


 

A tábla minden mezőjére ráírjuk, hogy arról a mezőről a futó hány más mezőt nem támad. Ezt könnyű elvégezni két észrevétel miatt: 1. Először azt számoljuk ki, hogy az adott mezőről futókkal hány másikra lehet átlépni, és ezt az értéket kell kivonnunk 63-ból. 2. Kihasználhatjuk a tábla középpontja körüli $ 90^\circ $-os forgatási és az átlókra való tükrözési szimmetriát, és így elég 10 mezőnél kiszámolni az értékeket. Ennyi helyre léphet át a futó Ennyi mezőt nem támad

7 7 7 7           56 56 56 56 56 56 56 56
  9 9 9           56 54 54 54 54 54 54 56
    11 11           56 54 52 52 52 52 54 56
      13           56 54 52 50 50 52 54 56
                  56 54 52 50 50 52 54 56
                  56 54 52 52 52 52 54 56
                  56 54 54 54 54 54 54 56
                  56 56 56 56 56 56 56 56

Most már ha elhelyezzük az ,,első futót'', akkor le tudjuk olvasni, hogy a ,,másodikat'' hányféleképpen helyezhetjük el. Az ,,elsőt'' a 64 mező bármelyikére tehetjük, így az ,,első'' és a ,,második'' futót összesen annyiféleképpen helyezhetjük el, amennyi a felírt 64 szám összege. Ez:

$ 56\cdot 28+54\cdot 20+52\cdot 12+50\cdot 4=3472. $

Valójában pont feleennyi lehetőség van, mert nincs ,,első'' és ,,második'' futó, hanem két egyforma futó van. Tehát a megoldás: 1736. Megjegyzés. Általánosíthatjuk a feladatot $ 2n\times 2n-$es táblára! Tekintsük az alábbi ábrát:

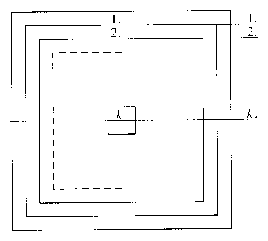
A $ 2n\times 2n$-es tábla mezőinek száma $ 4n^2$. Az egyes rétegekben lévő mezők száma rendre $i $=1, 2, ..., $n$ esetén:

$ \begin{array}{l} i=1\mbox{-re: }4\left( {2n} \right)-4 \\ i=2\mbox{-re: 4}\left( {\mbox{2}n\mbox{-2}} \right)-4 \\ i=3\mbox{-ra: 4}\left( {\mbox{2}n\mbox{-4}} \right)-4 \\ \mbox{ }\vdots \\ i\mbox{-re: 4}\left[ {\mbox{2}n-\left( {i-1} \right)\cdot 2} \right]-4=4\left( {2n-2i+1} \right) \\ \mbox{ }\vdots \\ i=n\mbox{-re: 4}\left[ {2n-\left( {n-1} \right)\cdot 2} \right]-4. \\ \end{array} $

Az $i$-edik rétegben álló futó (tetszőleges mezőn állva) rendre a következő számú mezőt foglalja el:

$ \begin{array}{l} i=1\mbox{-re: }2n+0\cdot 2 \\ i=2\mbox{-re: }2n+1\cdot 2 \\ i=3\mbox{-ra: }2n+2\cdot 2 \\ \mbox{ }\vdots \\ \end{array} $

tetszőleges $i\mbox{-re: }2n+\left( {i-1} \right)\cdot 2$

$ \begin{array}{l} \mbox{ }\vdots \\ i=n\mbox{-re: }2n+\left( {n-1} \right)\cdot 2 \\ \end{array} $

Javasoljuk, hogy rajzolja fel az olvasó az $i$-edik réteg tetszőleges mezőjén álló futó által elfoglalt mezőket! A megoldások $M$ száma az előzőek alapján --- az első megoldás gondolatmenetét követve ---:

$ M=\frac{1}{2}\sum\limits_{i=1}^n {4\left( {2n-2i+1} \right)} \left[ {4n^2-2n-\left( {i-1} \right)2} \right]= $
$ =4\sum\limits_{i=1}^n {\left( {2n-2i+1} \right)} \left( {2n^2-n+1-i} \right)= $
$ =4\sum\limits_{i=1}^n {\left( {2n+1} \right)} \left( {2n^2-n+1} \right)-4\sum\limits_{i=1}^n {\left( {4n^2+3} \right)} i+4\sum\limits_{i=1}^n {2i^2} $

Felhasználva, hogy $\sum\limits_{i=1}^n {i=\frac{n\left( {n+1} \right)}{2}} $ és

$ \sum\limits_{i=1}^n {i^2} =\frac{n\left( {n+1} \right)\left( {2n+1} \right)}{6} $
$ M=4n\left( {2n+1} \right)\left( {2n^2-n+1} \right)-2n\left( {n+1} \right)\left( {4n^2+3} \right)+\frac{4\cdot n\left( {n+1} \right)\left( {2n+1} \right)}{3}. $

Azonos átalakítások után az

$ M=\frac{2n\left( {12n^3-8n^2+3n-1} \right)}{3} $

eredményhez jutunk. Természetesen $n=4$-re a már ismert

$ M=\frac{8\cdot \left( {12\cdot 64-8\cdot 16+12-1} \right)}{3}=1736 $

megoldást kapjuk. A továbbiakban egy rekurzióra épülő általános megoldást is bemutatunk. Legyen a megfelelő elhelyezések száma $n\times n$-es tábla esetén $f\left( n \right)$. Jelöljük továbbá $g\left( n \right)$-nel azon elhelyezések számát, amelyekben mindkét futó a tábla szélső mezőjén áll, $h\left( n \right)$ pedig jelölje azoknak a megfelelő elhelyezéseknek a számát, amelyekben pontosan az egyik futó áll a tábla szélső mezőjén. Tekintsük a következő ábrát:

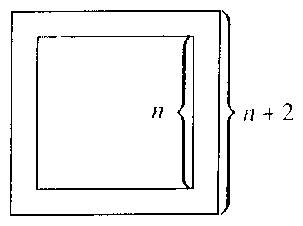
Ha az először letett futó sarokmezőre kerül, akkor $g\left( {n+2} \right)$-t tekintve a második futó már csak $ 4n+2$ helyre kerülhet. Ha viszont az ,,első'' futó nincs sarokmezőn --- ekkor $ 4n$ különböző mezőre kerülhet ---, akkor a második futó $ 4n+1$ darab mezőre állhat. Ezek alapján

$ g\left( {n+2} \right)=\frac{1}{2}\left[ {4\cdot \left( {4n+2} \right)+4\cdot \left( {4n+1} \right)} \right]=2\left( {4n^2+5n+2} \right), $

mert minden esetet kétszer vettünk számításba. Hasonló gondolatmenet alapján adódik a $h\cdot \left( {n+2} \right)$-re kapható $h\left( {n+2} \right)=4n^3$ formula, hiszen ha az egyik futó sarokmezőn áll, akkor a megfelelő esetek száma $ 4\left( {n^2-n} \right)$, ha pedig nem áll futó a sarokban, akkor $ 4n\left[ {n^2-\left( {n-1} \right)} \right]$ az elhelyezések száma. Ábránk és az eddigiek alapján nyilvánvaló, hogy $f\left( {n+2} \right)=f\left( n \right)+g\left( {n+2} \right)+h\left( {n+2} \right)$. Felhasználva, hogy $g\left( {n+2} \right)=2\left( {4n^2+5n+2} \right)$ és $h\left( {n+2} \right)=4n^3$, $f\left( {n+2} \right)$-re

$ f\left( {n+2} \right)=f\left( n \right)+4n^3+8n^2+10n+4 $

adódik. Ezzel $f\left( n \right)$ értékét sikerült rekurzív módon megadni. Ha például $f\left( 8 \right)$-at akarjuk kiszámítani (az eredeti feladat), akkor $f\left( 2 \right)=4$ alapján $f\left( 4 \right)=32+32+20+4+4=92,$ továbbá $f\left( 6 \right)=256+128+44+92=520,$ így

$ f\left( 8 \right)=4\cdot 6^3+8\cdot 6^2+64+520=1736, $

az első megoldásnak megfelelően. Megjegyezzük, hogy az $f\left( n \right)$-re kapott formula természetesen páratlan $n $értékek esetén is helyes, a rekurzió ,,kezdőértéke'' $f\left( 1 \right)=0$. Próbáljuk most meg egy lépésben megadni $f\left( {n+1} \right)$ értékét $f\left( n \right)$ segítségével! Alkalmazzuk a következő táblára rekurzív megadásunk gondolatmenetét:

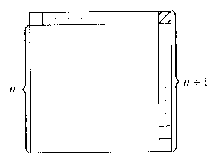
Ha mindkét futó az L alakú tartomány mezőin áll, akkor a megfelelő elhelyezések száma: $\frac{1\cdot 2n+2n\cdot \left( {2n-1} \right)}{2}=2n^2$, ha pedig pontosan az egyik futó áll az iménti tartomány egyik mezőjén, akkor

$ 1\cdot \left( {n^2-n} \right)+2n\cdot \left[ {n^2-\left( {n-1} \right)} \right]=2n^3-2n^2+n $

számú jó elhelyezés létezik. Az előzőek alapján ekkor

$ f\left( {n+1} \right)=f\left( n \right)+2n^2+2n^3-n^2+n=f\left( n \right)+2n^3+n^2+n. $

Tehát bármely $\left( {n+1} \right)\times \left( {n+1} \right)$-es táblára igaz, hogy a megfelelő futóelhelyezések számára teljesül az

$ f\left( {n+1} \right)=f\left( n \right)+2n^3+n^2+n $

összefüggés. Kapott eredményünk lehetőséget nyújt arra, hogy $f\left( n \right)$ értékét zárt alakban kapjuk meg. Bebizonyítjuk, hogy bármely $n\ge 1$ esetén

$ f\left( n \right)=\frac{\left( {n-1} \right)\cdot n\cdot \left( {3n^2-n+2} \right)}{6}. $

A bizonyításhoz vezessük be a következő jelölést:

$ S_n^{\left( k \right)} =1^k+2^k+3^k+\ldots +n^k $

Az $f\left( {n+1} \right)$-re kapott formula alapján

$ \begin{array}{l} f\left( 2 \right)=f\left( 1 \right)+2\cdot 1^3+1^2+1 \\ f\left( 3 \right)=f\left( 2 \right)+2\cdot 2^3+2^2+2 \\ f\left( 4 \right)=f\left( 3 \right)+2\cdot 3^3+3^2+3 \\ \mbox{ }\vdots \\ f\left( {n+1} \right)=f\left( n \right)+2\cdot n^3+n^2+n. \\ \end{array} $

A felírt $n$ darab összefüggés megfelelő oldalainak összegzésével az

$ f\left( {n+1} \right)-f\left( 1 \right)=2S_n^{\left( 3 \right)} +S_n^{\left( 2 \right)} +S_n^{\left( 1 \right)} $

egyenlőséghez jutunk, ahol $f\left( 1 \right)=0$. Felhasználva, hogy

$ S_n^{\left( 3 \right)} =\frac{n^2\left( {n+1} \right)^2}{4}, $

$S_n^{\left( 2 \right)} =\frac{n\left( {n+1} \right)\left( {2n+1} \right)}{6}$ és

$ S_n^{\left( 1 \right)} =\frac{n\left( {n+1} \right)}{2} $

azonos átalakítások után a bizonyítandó

$ f\left( {n+1} \right)=\frac{n\left( {n+1} \right)\left( {3n^2+5n+4} \right)}{6} $

formulához jutunk, ahonnan $\left( {n+1} \right)$ helyett $n$-et írva

$ f\left( n \right)=\frac{\left( {n-1} \right)\cdot n\cdot \left( {3n^2-n+2} \right)}{6} $

adódik. Végezetül egy további általánosítási lehetőséget vizsgálunk meg. Kérdésünk az, hogy az $n\times k-$as táblán ($n$ darab oszlop és $k$ darab sor) $n\ge k$ esetén mennyi a megfelelő futóelhelyezések száma. Az $f\left( {n+1} \right)$-re kapott formula esetében alkalmazott gondolatmenet alapján:

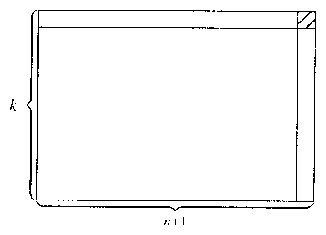
$ f\left( {n+1,k} \right)=f\left( {n,k} \right)+\frac{k\left( {k-1} \right)}{2}+k\left[ {nk-\left( {k-1} \right)} \right], $

azaz

$ f\left( {n+1,k} \right)=f\left( {n,k} \right)+n\cdot k^2-\frac{k\left( {k-1} \right)}{2} $

Eredményünk alapján

$ \begin{array}{l} f\left( {k+1,k} \right)=f\left( {k,k} \right)+k\cdot k^2-\frac{k\left( {k-1} \right)}{2} \\ f\left( {k+2,k} \right)=f\left( {k+1,k} \right)+\left( {k+1} \right)\cdot k^2-\frac{k\left( {k-1} \right)}{2} \\ f\left( {k+3,k} \right)=f\left( {k+2,k} \right)+\left( {k+2} \right)\cdot k^2-\frac{k\left( {k-1} \right)}{2} \\ \mbox{ }\vdots \\ f\left( {k+l,k} \right)=f\left( {k+l-1,k} \right)+\left( {k+l-1} \right)\cdot k^2-\frac{k\left( {k-1} \right)}{2} \\ \end{array} $

A felírt egyenlőségek összegzésével

$ f\left( {k+l.k} \right)=f\left( {k,k} \right)+k^2\left[ {k+\left( {k+1} \right)+\left( {k+2} \right)+...+\left( {k+l-1} \right)} \right]-\frac{k\left( {k-1} \right)}{2}\cdot l $

adódik, ahonnan rendezéssel

$ f\left( {k+l,k} \right)=f\left( {k,k} \right)+\frac{k\cdot l}{2}\left( {2k^2+kl-2k+1} \right) $

Ha tehát $n\ge k$ és $n=k+l$ jelöléssel élünk, akkor

$ f\left( {n,k} \right)=f\left( {k+l,k} \right)=f\left( {k,k} \right)+\frac{k\left( {n-k} \right)}{2}\left( {k^2+nk-2k+1} \right) $

Formulánkba $f\left( {k,k} \right)=\frac{\left( {k-1} \right)\cdot k\cdot \left( {3k^2-k+2} \right)}{6}$-ot helyettesítve azonos átalakítások után az

$ f\left( {n,k} \right)=\frac{\left( {k-1} \right)k\left( {3k^2-k+2} \right)}{6}+\frac{k\left( {n-k} \right)}{2}\left( {k^2+nk-2k+1} \right)= $
$ =\frac{3nk\left( {nk-2k+1} \right)+2\left( {k-1} \right)k\left( {k+1} \right)}{6} $

eredményt kapjuk. Ezzel feladatunkat bármilyen $n\times k$-as táblára megoldottuk, hiszen $k>n$ esetén (a tábla szimmetriája miatt) $n$ és $k$ szerepcseréjével jutunk a megfelelő eredményhez.