Egy 30 fős osztály matematikaérettségi vizsgájának érdemjegyei olvashatók le az alábbi diagramról.

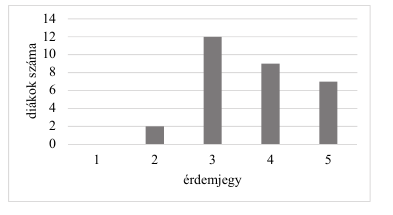
a)Adja meg az osztály matematikaérettségi érdemjegyeinek átlagát, mediánját és móduszát!

b) Ábrázolja az érdemjegyek eloszlását kördiagramon!

Az osztály tanulóinak matematikaérettségi dolgozatai közül az érettségi elnök véletlenszerűen kiválaszt és megvizsgál kettőt.

c) Számítsa ki annak a valószínűségét, hogy mindkét kiválasztott dolgozat érdemjegye hármas! Válaszát három tizedesjegyre kerekítve adja meg!

Megoldás:  a) Átlag: $ 3,7$; medián: $ 4 $; módusz: $ 3$

b) 1 főnek $ 12^\circ $-os középponti szög felel meg az ábrán. Az egyes osztályzatokhoz tartozó középponti szögek: 2-es: $ 24^\circ $; 3-as: $ 144^\circ $; 4-es: $ 108^\circ $; 5-ös: $ 84^\circ $.

c) $P=\dfrac{132}{870}\approx 0,152$