Anna dominókészletében a dominókövek egyik oldala egy vonallal két részre van osztva. Az egyes részeken a pöttyök száma 0, 1, 2, 3, 4, 5 vagy 6 lehet. A készletben minden lehetséges pöttyözésű dominóból pontosan egy darab van. Az ábrán a 2-6-os (6-2-es) dominó látható.

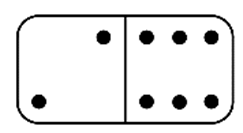
a) Hány olyan dominó van a készletben, amelyen a két részen lévő pöttyök számának szorzata prímszám?

A játékban két dominó akkor csatlakozhat egymáshoz, ha a két érintkező részen ugyanannyi pötty van. (Lásd az ábrát.)

Anna egy lapra elhelyezte dominókészletének azt a hat dominóját, amelyek mindkét részén van legalább 1, de legfeljebb 3 pötty. Ezután összekötötte azokat a dominókat, amelyeket a játékban csatlakoztatni lehetne egymáshoz. Az alábbi ábra a hat dominót és az összekötő vonalakat mutatja, de csak két részen adtuk meg a pöttyöket.

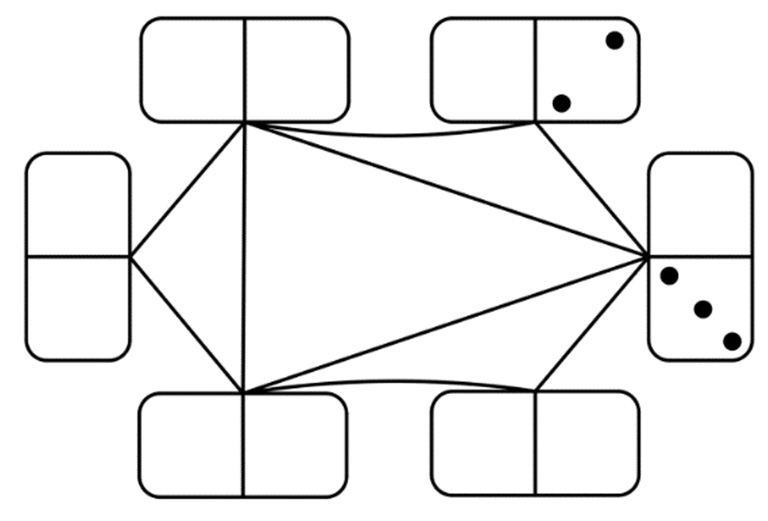
b) Rajzolja be a tíz üres részre a hiányzó pöttyöket az összekötésnek megfelelően! Anna a teljes 28 darabos készletből kihúzta a 2-6-os dominót. Ezután véletlenszerűen kihúz még egy dominót.

c) Számítsa ki annak a valószínűségét, hogy a másodiknak kihúzott dominót csatlakoztatni tudja az elsőhöz!

Egy játékbemutatóra Anna és Balázs 1800 dominót szeretne felállítani a földre úgy, hogy a legelsőt meglökve az összes dominó sorban eldőljön. Anna egyedül 6 óra alatt, Balázs pedig 9 óra alatt építené meg a dominóláncot.

d) Ha Anna és Balázs – tartva a saját tempójukat – együtt dolgozna, akkor hány óra alatt végeznének az 1800 dominó felállításával?

Megoldás:

a) Összesen három ilyen dominó van a készletben.

b) A hat megrajzolt dominó: 1-1, 2-1, 3-1, 2-2, 3-2 és 3-3.

c) $ P=\dfrac 4 9$

d) Anna és Balázs együtt dolgozva 3,6 óra alatt végeznek.