Az ábrán egy $ 3\times 3 $-as kirakós játék (puzzle) sematikus képe látható.

A kirakós játékot egy gráffal szemléltethetjük úgy, hogy a gráf csúcsai (A1, A2, ... , C3) a puzzle-elemeket jelölik, a gráf két csúcsa között pedig pontosan akkor vezet él, ha a két csúcsnak megfelelő puzzle-elemek közvetlenül (egy oldalban) kapcsolódnak egymáshoz a teljesen kirakott képben.

a) Rajzolja fel a kirakós játék gráfját (a csúcsok azonosításával együtt), és határozza meg a gráfban a fokszámok összegét!

b) Igazolja, hogy a megrajzolt gráfban nincs olyan (gráfelméleti) kör, amely páratlan sok élből áll!

c) A teljesen kirakott képen jelöljön meg a puzzle-elemek közül 7 darabot úgy, hogy a kirakósjáték általuk alkotott részlete (a részletnek megfelelő gráf) már ne legyen összefüggő!

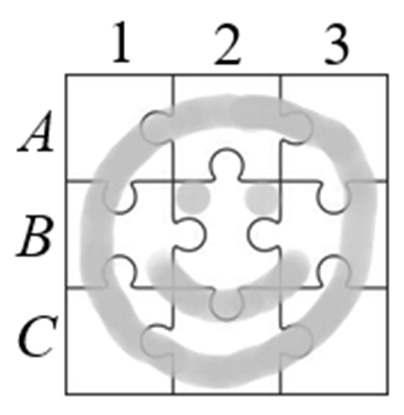
d) Hányféleképpen lehet a puzzle-elemek közül hármat úgy kiválasztani, hogy ezek a teljesen kirakott képben kapcsolódjanak egymáshoz (azaz mindhárom képrészlet közvetlenül kapcsolódjék legalább egy másikhoz a kiválasztottak közül)? (Az elemek kiválasztásának sorrendjére nem vagyunk tekintettel.)

Megoldás:

a) --

b) --

c) --

d) 22