A római katonák az úgynevezett taxillus-szal játszottak "kockajátékot". (A taxillus a keske vagy a juh térdkalácsából faragott csontocska; ld. a képen.)

Dobás után egy taxillus négy különböző oldalára eshetett. Jelölje ezt a négy különböző helyzetet A, B, C és D. Az egyes dobáskimenetelek nem voltak egyformán valószínűek: az A, illetve a B helyzet egyaránt $ \dfrac{4}{10} $, a C, illetve a D helyzet pedig egyaránt $ \dfrac{1}{10} $ valószínűséggel következett be. A rómaiak általában négy taxillust dobtak fel egyszerre. A Venus-dobás volt az egyik legértékesebb, ekkor a négy csontocska mindegyike más-más oldalára esett.

a) Mennyi a Venus-dobás valószínűsége?

b) Az alábbi két esemény közül melyiknek nagyobb a valószínűsége?

I. Négy feldobott taxillus között lesz olyan, amelyik C helyzetben érkezik le.

II. Négy feldobott taxillus között pontosan egy érkezik le az A helyzetben.

Thalész, a hét görög bölcs egyike, egy nevezetes, neki tulajdonított mérés során egy folyóban lévő sziget AB hoszszát a folyóparton maradva határozta meg.

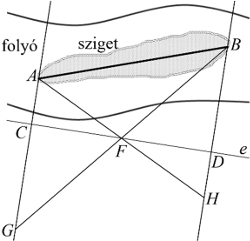
Először felvett egy e egyenest a parton. Ezen az e egyenesen megkereste azt a C, illetve D pontot, amelyekben a CA, illetve a DB irány merőleges az e egyenesre. Ezután a CD szakasz F felezőpontját is megjelölte egy jelzőkaróval. Ezt követően az AC egyenesen haladva megjelölte azt a G pontot, amelyre B, F és G egy egyenesre illeszkedik; és hasonlóan az AF és BD egyenesek H metszéspontját is megjelölte. Thalész azt állította, hogy a sziget hossza a GH távolsággal egyezik meg.

c) Igazolja Thalész állításának helyességét!

Megoldás:

a) $\dfrac{24}{625}$

b) A II. esemény valószínűbb, mint az I.

c) -