Az $ ABCDEFGH $ négyzetes oszlop $ AE $, $ BF $, $ CG $, $ DH $ élei merőlegesek az $ ABCD $ alaplapra. Az $ A $ csúcsból kiinduló három él hossza $ AB = AD = 8$ egység, $AE=15$ egység.

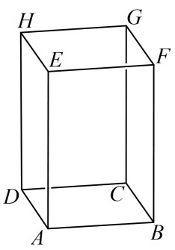
a) Számítsa ki az $ \overline{EF }$ és $ \overline{AH }$ vektorok skaláris szorzatát!

A négyzetes oszlop köré egy $P $ csúcspontú forgáskúpot illesztünk úgy, hogy az $ A $, $ B $, $ C $, $ D $ csúcsok a kúp alaplapjára, az $ E $, $ F $, $ G $, $ H $ csúcsok pedig a kúp palástjára illeszkedjenek. (A kúp és a négyzetes oszlop tengelye egybeesik.) A kúp magassága 45 egység.

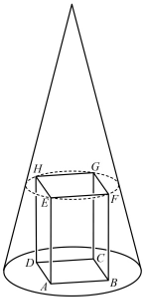
b) Számítsa ki a kúp felszínét!

c) Hány olyan derékszögű háromszög van, amelynek egyik befogója $ 15 $ egység hosszú, és a másik két oldala is egész szám hosszúságú? (Az egybevágó háromszögeket nem tekintjük különbözőknek.)

Megoldás:

a) $ 0$, mert merőlegesek

b) $ \approx 1446,9$

c) 4 háromszög van