Egy konvex testnek két háromszöglapja és három négyszöglapja van. Kössük össze az egyik háromszöglap mindegyik csúcsát a vele szemközti négyszöglap átlóinak metszéspontjával. Bizonyítsuk be, hogy három egyenes egy ponton megy át.

Meg kell határoznunk a test alakját. Egy négyszöglap éleihez csatlakozik mind a négy további lap. Mivel a test konvex, így a testet a négyszöglapok síkjai által határolt egyik konvex térrészből a háromszöglapok síkjai metszik ki.

Legyenek ezek a lapok $A_1 B_1 C_1 $ és $A_2 B_2 C_2 $, a további élek pedig $A_1 A_2 $, $B_1 B_2 $, $C_1 C_2 $ (2. ábra). Jelöljük a $B_1 B_2 C_2 C_1 $, $C_1 C_2 A_2 A_1 $, $A_1 A_2 B_2 B_1 $ lapok átlóinak a metszéspontját rendre $A_3 $, $B_3 $, $C_3 $-mal, és nézzük az $A_1 A_3 $, $B_1 B_3 $, $C_1 C_3 $ egyeneseket.

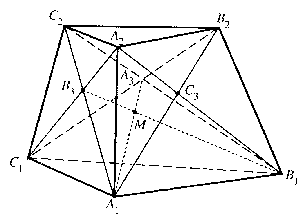
Az $A_1 B_1 C_2 $ síkmetszet $B_1 C_2 $ oldalának belső pontja $A_3 $, $A_1 C_2 $-nek pedig $B_3 $, így $A_1 A_3 $ és $B_1 B_3 $ metszi egymást a háromszög belsejének egy $M$ pontjában. Hasonlóan látható, hogy $C_1 C_3 $ is metszi $A_1 A_3 $-at is, $B_1 B_3 $-at is. Az $A_1 B_1 C_2 $ síknak egyik oldalára esik $C_1 $, a másikra $A_2 $ és $B_2 $, tehát $C_1 $ és $C_3 $ is ellenkező oldalára esik. $C_1 C_3 $-nak tehát egy közös pontja van a síkkal, és így csak akkor metszheti $A_1 A_3 $-at is, $B_1 B_3 $-at is, ha ez a pont $M$. A három egyenes tehát egy ponton megy keresztül, és ezt kellett bizonyítanunk. 

Megjegyzések: 

1. A feladat megoldását többen arra a tételre hivatkozva fejezték be, hogy ha három egyenes páronként metszi egymást, akkor vagy egy síkban vannak, vagy egy ponton mennek keresztül Ez igaz három helyett akárhány (de legalább 3) egyenesre, és így látható be. Ha egy ponton mennek át az egyenesek, akkor igaz az állítás. Ha ez nem áll, akkor vegyünk egy $P$ metszéspontot. Egy $e$ egyenes, amelyik nem megy át $P$-n, a $P$-n átmenő egyeneseket (tehát legalább két egyenest) $P$-től különböző pontban metsz. Ekkor azonban a $P$-n átmenő egyenesek benne vannak a $P$ és $e$ által meghatározott síkban. Ebben a síkban minden további egyenes is benne van, hiszen különböző pontokban metsz legalább két $P$-n átmenő egyenest.

2. A feladat megoldásában valójában három metsző síkról van szó, az $A_1 B_1 C_2 $ háromszögén kívül az $A_1 B_2 C_1 $ és az $A_2 B_1 C_1 $ háromszög síkjáról. A fenti megoldás egy változatához jutunk, ha azt látjuk be, hogy $A_1 A_3 $, $B_1 B_3 $ és $C_1 C_3 $ közül rendre két-két sík metszésvonala, és ezek nem lehetnek párhuzamosak.

3. Bár a megoldás során ismételten hivatkoztunk a test konvex voltára, ez többnyire csak bizonyos metszéspontok létrejöttének a biztosításához kellett. Felmerül a kérdés, hogy ez nem biztosítható-e egyszerűbb feltételekkel is. Ennek végiggondolását az olvasóra hagyjuk.

4. A feladat megfogalmazható síkbeli feladatként, csak azt kell figyelembe venni, hogy a test alakját vizsgálva arra jutottunk, hogy $A_1 A_2 $, $B_1 B_2 $ és $C_1 C_2 $ egy ponton megy keresztül, vagy párhuzamosak. A megfelelő síkbeli feladat tehát így szól: Az $A_1 A_2 $, $B_1 B_2 $, $C_1 C_2 $ egyenesek egy ponton mennek keresztül, vagy párhuzamosak. $A_1 B_2 $ és $B_1 A_2 $, $B_1 C_2 $ és $C_1 B_2 $, $C_1 A_2 $ és $A_1 C_2 $ metszéspontját sorra $C_3 $, $A_3 $, $B_3 $-mal jelölve bizonyítandó, hogy $A_1 A_3 $, $B_1 B_3 $ és $C_1 C_3 $ egy ponton mennek keresztül, vagy párhuzamosak. (Feltesszük, hogy $A_3 $, $B_3 $ és $C_3 $ létrejön.) A bizonyításra kényelmes út az ábrát térbeli alakzat vetületének fogni fel. Egy síkban maradó bizonyítás igen nehéznek látszik.