Tekintsük az $ A $, $ B $, $ C $, $ D $ és $ E $ pontokat egy gráf csúcsainak.

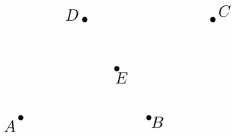
a) Egészítse ki élekkel a fenti ábrát úgy, hogy a kapott gráfban minden csúcs fokszáma 2 vagy 3 legyen!
b) Lehet-e olyan 5 csúcsú gráfot rajzolni, amelyben minden csúcs fokszáma pontosan 3?
Az $ A $, $ B $, $ C $, $ D $ pontok egy paralelogrammát alkotnak, az $ E $ pont az átlók metszéspontja.

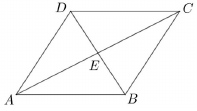
c) Fejezze ki az $ \overrightarrow{AB} $ vektort a $ \overrightarrow{DA} $ és $ \overrightarrow{DE} $ vektorok segítségével!
Egy $ ABCD $ paralelogrammát elhelyeztünk a koordináta-rendszerben. Tudjuk, hogy az $ AB $  egyenes egyenlete $ 2x - 5y = - 4 $ , az $ AD $ egyenes egyenlete pedig $ 3x - 2y = - 6 $. A $ C $ pont koordinátái $ (5; 5) $, a $ B $ pont első koordinátája $ 3 $.
d) Határozza meg a paralelogramma $ A $, $ B $ és $ D $ csúcsának koordinátáit!

Megoldás:

a) Egy megfelelő gráf
b) Ilyen gráf nincs

c) $ \overrightarrow{AB} = -  \overrightarrow{DA} + 2\cdot \overrightarrow{DE} $

d) $  A(-2; 0);\  B(3; 2);\  D(0; 3) $