Adott négy, a valós számok halmazán értelmezett függvény:

$  f(x) = (x + 4)(2 - x);\qquad g(x) = x + 4 $

$ h(x) = x^2 - 4;\qquad (x) = \left| x \right| - 4 $

a) Határozza meg az $ f $ és $ g $ függvények grafikonja által közrezárt korlátos síkidom területét!
Egy négypontú gráf csúcsait megfeleltetjük e négy függvénynek. Két csúcsot pontosan akkor kötünk össze éllel, ha a két megfelelő függvénynek van közös zérushelye.
b) Rajzolja fel az így kapott gráfot!
A valós számok halmazán értelmezett $ k $ függvény zérushelyei $ -5 $ és $ 3 $, az $ m $ függvény zérushelyei $ 3 $ és $ -3 $, az $ n $ függvény zérushelyei pedig $ 5 $ és $ -5 $. A $ p $ elsőfokú függvény hozzárendelési szabálya $ p(x) = x + c $, ahol $ c $ egy valós szám.
c) Hányféleképpen választható meg a $ c $ konstans értéke úgy, hogy a $ k $, $ m $, $ n $ és $ p $ függvényekre a b) feladatban megadott szabály szerint elkészített négypontú gráf fagráf legyen?

Megoldás:

a) $ t = \dfrac{125}{6} $

b) 

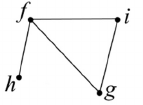
c) Kétféleképpen választható