Az $ ABC $ szabályos háromszög mindhárom oldalát 3-3 osztóponttal négy egyenlő részre osztottuk.

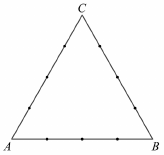a) Hány olyan négyszög van, melynek mind a négy csúcsa a háromszög oldalain kijelölt 9 pont közül való úgy,
hogy a négyszögnek a háromszög mindegyik oldalán van legalább egy csúcsa? (Két négyszöget különbözőnek tekintünk, ha legalább egy csúcsukban különböznek.)
Jelölje a 4 egység oldalú $ ABC $ szabályos háromszög $ BC $ ol dalának $ B $-hez közelebbi negyedelőpontját $ P $, a $ CA $ oldal  $ C $-hez közelebbi negyedelőpontját $ Q $, az $ AB $ oldal $ A $-hoz közelebbi negyedelőpontját pedig $ R $. Jelölje továbbá $ AP $ és $ BQ $  szakaszok metszéspontját $ X $, $ BQ $ és $ CR $ szakaszok metszéspontját $ Y $, végül $ CR $ és $ AP $ szakaszok metszéspontját $ Z $.

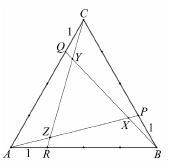
b) Határozza meg az $ XYZ $ vháromszög területét!

Megoldás:

a) 81

b) $ \approx 2,13 $