Egy síkbeli terepen hat város között 6 út vezet. Az első $A_{1}$-ből $B_{1 }$--be, a második $A_{2}$-ből $B_{2 }$--be, a harmadik pedig $A_{3}$-ből $B_{3 }$--ba. $A_{i}$-ből ($ i$ = 1, 2, 3) egyszerre indul el $f_{i}$ futár ( $i$ = 1, 2, 3) a $B_{i}$ városba ( $i$ = 1, 2, 3), ahol mindegyik futár állandó sebességgel halad. A közös indulás után $a$ óra elteltével $f_{1}$ és $f_{2}$ találkozik, majd ezután $b$ óra elteltével $f_{1}$ és $f_{3}$ találkozik, majd ismét $a$ óra elteltével $f_{2}$ és $f_{3 }$mennek el egymás mellet, végül újabb $b$ óra múlva mindhárman egyszerre érnek célba. Milyen messze lehet $B_{1} \quad B_{3 }$--tól, ha $a \quad >$ 0, $b \quad >$ 0 és $A_{1}A_{2}$ = 1km?

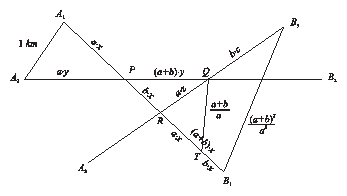
Legyen $f_{1 }$futár sebessége $x$,$ f_{2}$-é $y$, és $f_{3}$-é $z$. $f_{1}$ és $f_{2}$ találkozzon a $P$ pontban, $f_{1}$ és $f_{3}$ az $R$ pontban, $f_{2}$ és $f_{3}$ a $Q$ pontban. Így az $A_{1}P$ szakasz hossza $a\cdot x$, a PR szakasz hossza $b\cdot x$, a RB$_{1}$ szakasz hossza $(a+b)\cdot x$ , az $A_{2}P$ szakasz hossza $a\cdot y$, a PQ szakasz hossza $(a+b)\cdot y$, a QB$_{3}$ szakasz hossza $b\cdot z$, a QR szakasz hossza $a\cdot z$. Legyen $T$ a QB$_{1}$ szakasz $a$:$b$ arányú osztópontja. Mivel az $A_{1}$PA$_{2}$ és a QPT szög egyenlő nagyságú, és a közrefogó oldalak aránya megegyezik, ezért az $A_{1}$PA$_{2}$ és a QPT háromszög hasonló, a hasonlóság aránya $a$:($a+b)$. Ennek alapján az RT szakasz hossza $\frac{a+b}{a}$. A QRT és a $B_{3}$RB$_{1}$ háromszögben a $B_{3}$RB$_{1}$ és a QRT szög és a közrefogó oldalak aránya megegyezik, ezért ez a két háromszög is hasonló. A hasonlóság aránya $a$:($a+b)$, ezért a $B_{1}B_{3}$ szakasz hossza