Adott a síkban egy egyenes, égy $n$ cm sugarú kör ($n$ egész szám) és a körben 4$n$ darab 1 cm-es szakasz. Bizonyítsuk be, hogy húzható az adott egyenessel párhuzamosan vagy rá merőlegesen olyan húr, amelynek legalább két szakasszal van közös pontja.

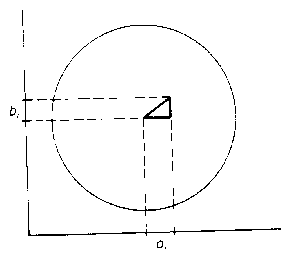
Vetítsük a 4$n$ szakasz mindegyikét az adott egyenesre (ezt vízszintesnek mondjuk) és egy rá merőleges (függőlegesnek mondott) egyenesre. A vízszintes vetületek hossza legyen $a_{l}$, $a_{2}$,$ ... , a_{4n}, $a függőlegeseké pedig $b_{1}, b_{2}, $..., $b_{4n}$. A feladat állítása egyértelmű azzal a kijelentéssel, hogy vagy a vízszintes, vagy a függőleges vetületek között van kettő, amelyeknek van közös pontja. Az $i$-edik szakasz olyan (esetleg szakasszá elfajuló) derékszögű háromszög átfogója, amelynek vízszintes befogója $a_{i}$, függőleges befogója pedig $b_{i}$ hosszúságú (1. ábra). Minthogy a háromszög két oldalának összege a harmadiknál nagyobb, $a_{i} + b_{i} \quad \ge {\rm B}$ 1$.$

Itt az egyenlőséget is meg kellett engednünk, mert számolunk azzal, hogy a vetített szakasz vízszintes vagy függőleges. Eredményünkből következik, hogy mind a 4$n $szakasz vetületeinek összege $\Sigma a_{i} + \Sigma b_{i} \quad \ge {\rm B}$ 4$n$. Itt és a következőkben is minden összegezés az $i$ = 1, 2, ..., 4$n$ értékekre terjed ki. Ha a vízszintes vetületek között nincs két közös pontú, akkor ezek együttesen nem fedik le az$ n $sugarú kör 2$n $hosszúságú vízszintes vetületét, tehát $\Sigma a_{i} $< \quad 2$n.$ Ugyanígy, ha a függőleges vetületek között nincs két közös pontú, akkor $ \Sigma b_{i} $< \quad 2$n.$ Ha tehát egyik eset sem következik be, akkor $\Sigma a_{i} + \Sigma b_{i} $< \quad 4$n$. Ez ellentmond fenti eredményünknek. Kell tehát, hogy a mondott két eset valamelyike bekövetkezzék, ami - mint megállapítottuk - a feladat állításának helyességét mondja ki.
Megjegyzés. A feladat megoldásakor zárt szakaszokra gondoltunk. azaz a szakaszokhoz végpontjaikat is hozzászámítottuk. Igaz a feladat állítása nyílt, tehát végpontjaiktól megfosztott szakaszokra is, ennek bizonyításához azonban ki kell egészítenünk megoldásunkat. Ha nyílt szakaszokkal dolgozunk, akkor a kör 2$n$ hosszúságú vetületén elhelyezkedő, közös pont nélküli vetületi szakaszok hosszának összege 2$n$ is lehet, hiszen most a végpontjukkal érintkező szakaszoknak nincs közös pontja. Így tehát csak $\Sigma a_{i }\le {\rm A}$ 2$n$, $\Sigma b_{i }\le {\rm A}$ 2$n$ és ezekből $\Sigma a_{i }+\Sigma b_{i }\le {\rm A}$ 4$n$ eredményhez juthatunk, ami nem jelent ellentmondást.

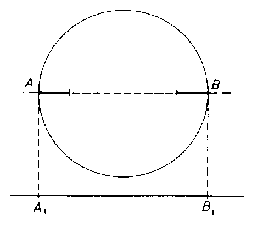
Ha azonban így nem jutunk ellentmondáshoz, tehát a feladat állításának bizonyításához sem, akkor $\Sigma a_{i }+\Sigma b_{i }$= 4$n$, tehát $\Sigma a_{i }$= 2$n$. Ez azt jelenti, hogy a vízszintes vetületek (végpontjaikkal együtt) a kör teljes vízszintes vetületét, az $A_{1}B_{1}$ szakaszt beborítják (2. ábra). Ekkor a vetületek között van $A_{1 }$kezdőpontú és $B_{1}$ végpontú is. Ilyen vetületet azonban csak a kör vízszintes AB átmérőjén elhelyezkedő szakaszok adhatnak. Ebben az eddig el nem intézett esetben tehát az adott egyenessel párhuzamos AB egyenes kielégíti a feladat követelményét, hiszen nemcsak közös pontja van két szakasszal, hanem tartalmazza is azokat.