Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
Látogatók
Összes:
10 802 504 Mai:
703 18-97-14-90.crawl.commoncrawl.org
(IP: 18.97.14.90) HonlapokSULINET Matematika Oktatási Hivatal Versenyvizsga portál Matematika Portálok |
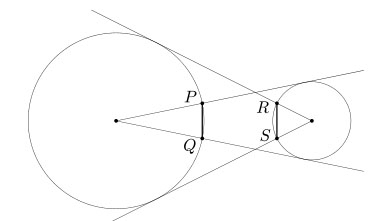
1. találat: ARANYD 2015/2016 Haladó I. kategória döntő 1. feladat Témakör: *Geometria (kör, érintő) (Azonosító: AD_20152016_h1kdf1f ) Két, nem metsző kör középpontjaiból érintőket húzunk a másik körhöz (lásd ábra). P , Q és R, S azok a pontok, ahol ezek az érintők metszik a köröket. Bizonyítsuk be, hogy PQ = RS.
Témakör: *Számelmélet (osztó) (Azonosító: AD_20152016_h1kdf2f ) Egy hatjegyű szám számjegyeinek szorzata 190 512. a) Hány ilyen szám van? b) Melyek ezek közül a négyzetszámok? Témakör: *Számelmélet (osztó) (Azonosító: AD_20152016_h1kdf3f ) 2016 db pozitív szám mindegyike a további 2015 négyzetösszegével egyenlő. Mekkora lehet a legkisebb szám értéke?
|
KeresésHonlapokKözépiskolai Matematikai és Fizikai Lapok Wolfram Alpha Art of Problem Solving Kvant IMO |
|||||||||||||||||
|
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
| |||||||||||||||||||
| |||||||||||||||||||
|
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
|
|
1082 Budapest, Horváth Mihály tér 8. OM azonosító: 035277 |
Joomla template: szsnjm4-001 (c) Szoldatics József 2011/2025
www.szolda.hu
www.szolda.hu