1. találat: ARANYD 2016/2017 HaladóIII. kategória 1. forduló 1. feladat
Témakör: *Geometria (kerület, terület, szélsőérték) (Azonosító: AD_20162017_h3k1f1f )
Adott egy AB szakasz, s rajta tetszőlegesen 2017 pont. A szakaszra az ábrán látható módon adott α szögű egyenlőszárú háromszögeket rajzolunk.
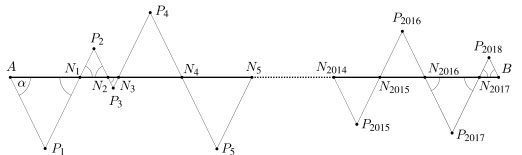
a) Hogyan vegyük fel a pontokat, hogy ezen háromszögek területeinek összege minimális legyen?
b) Hogyan vegyük fel a pontokat, hogy az AP1N1P2N2 . . . P2018B töröttvonal hossza a legnagyobb legyen?
*Geometria (Azonosító: AD_20162017_h3k1f2f )
A $BAC\sphericalangle$ belső szögfelezőjének egyik – A-tól különböző – pontja D. Bizonyítsuk be, hogy ha két kör közös metszéspontja A és D, akkor a $BAC\sphericalangle$ szög szárainak (AB és AC félegyenesek) a két kör közé eső szakasza ugyanolyan hosszú! Diszkutáljuk a feladatot!
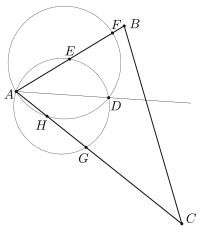
*Kombinatorika (Azonosító: AD_20162017_h3k1f3f )
10 egymást követő egész szám közül magányosnak nevezzük azokat, amelyek relatív prímek az összes többihez. Igazoljuk, hogy 10 egymást követő egész között mindig lesz legalább egy, ami magányos!
b) Mutassunk példát 10 szomszédos egészre, amelyek között pontosan egy magányos szám van!
*Algebra (gyökös) (Azonosító: AD_20162017_h3k1f4f )
Oldjuk meg a következő egyenletrendszert a valós számpárok halmazán:
$\begin{cases}\left(x-\sqrt{x^2+1}\right)\left(y-\sqrt{y^2+1}\right)=1\\ \left(x^2+y-2\right)\left(y^2+x-2\right)=-2\end{cases}$
*Kombinatorika (Azonosító: AD_20162017_h3k1f5f )
Ramszesznek, a fáraó írnokának van néhány egyforma nagyságú búzalepénye. Vallási előírásokból, ha egy lepényt felvágnak, akkor legfeljebb hét darab egyforma nagyságú részre kell vágni, és az egyszer már több részre osztott lepény darabjai tovább már nem oszthatóak. Igazoljuk, hogy ha Ramszesznek legalább 18 egyforma lepénye van, akkor szét tudja osztani olyan adagokra, hogy az egyiptomi holdhónap mind a 28 napjára egyforma mennyiségű lepény jusson!


