1. találat: Kavics Kupa 2008 1. feladat
Témakör: *Geometria (háromszög) (Azonosító: kk_2008_01f )
A nagyabonyi kocsma faasztalába valaki egy olyan háromszöget vésett, melynek oldalai (hüvelykben mérve) egymást követő egész számok. Ennek a háromszögnek a középső oldalához tartozó magassága két olyan részre osztja a középső oldalt, melyek különbsége x. Hány hüvelyknyi x?
*Algebra (Azonosító: kk_2008_02f )
Burkusföld határánál a burkus őr és a magyar silbak az unalom ellen kitalálós játékba kezdtek. A burkus őr olyan a és b pozitív egész számokra gondol, melyek egymásnak nem osztói, ám a kétezret mindketten osztják, továbbá. a
*Algebra (Azonosító: kk_2008_03f )
Miután az előző játékot megunták, a burkus határőr kardjával az alábbi számokat karcolta a hóba: 1, 1/2, 1/3, … 1/10. A magyar silbak letaposhat két hóbarajzolt, számot, a-t és b-t, de akkor helyettük oda kell karcolnia az a+b+ab számot. Meg is teszi, egymás után kilencszer, ami után már csak egy szám marad. Mennyi lehet ez a szám legfeljebb?
*Algebra (Azonosító: kk_2008_04f )
A burkus őrbódé egy szabályos nyolcszög alapú, egyenes hasáb. Miután átrántotta hazai földre, Háry megszámozza éleit 1-től 24-ig, majd megszámolja, hány olyan (rendezetlen) számpár van, melynek megfelelő élek kitérők. Hányat számolt?
*Geometria ( kör) (Azonosító: kk_2008_05f )
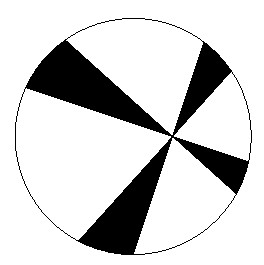 Mária Lujza a legújabb párizsi divat szerint kitűzőkkel díszíti báli ruháját. A legfurcsább közülük egy kör alakú kitűző, melynek átmérője 4 cm. Fehér alapon egy furcsa, fekete, kereszt-szerű alakzat látható rajta, melynek pontos leírását János így adta meg: a kitűző középpontjától 1 centire veszünk egy P pontot. Ezen az P-n át bocsátunk két, egymásra merőleges egyenest, majd ezeket 0,1 radiánnal elforgatjuk P körül. Éppen a forgatás közben az egyenesek által súrolt rész van feketére festve. Hány négyzetmilliméter a kereszt területe?
Mária Lujza a legújabb párizsi divat szerint kitűzőkkel díszíti báli ruháját. A legfurcsább közülük egy kör alakú kitűző, melynek átmérője 4 cm. Fehér alapon egy furcsa, fekete, kereszt-szerű alakzat látható rajta, melynek pontos leírását János így adta meg: a kitűző középpontjától 1 centire veszünk egy P pontot. Ezen az P-n át bocsátunk két, egymásra merőleges egyenest, majd ezeket 0,1 radiánnal elforgatjuk P körül. Éppen a forgatás közben az egyenesek által súrolt rész van feketére festve. Hány négyzetmilliméter a kereszt területe?
*Geometria (Azonosító: kk_2008_06f )
Örzséjével hosszú órákat töltött János a császár csodás kertjében. A kertet öt egyenes, széles kocsiút szeli át. Bármely egyenes mentén, amely két kocsiút szögfelezője, halad egy gyalogösvény. Bárhol, ahol legalább két gyalogösvény keresztezi egymást, áll egy szökőkút. Máshol nem lehet szökőkút, csakkereszteződéseknél. Legfeljebb hány szökőkút lehet a császár parkjában?
*Geometria (Azonosító: kk_2008_07f )
Egyszer egy hatalmas gyémántot hoztak Bécsbe a bányászok. A bánya azonban éppen háborús területen volt, így Napóleon és Ferenc császár is magáénak követelte. Háry azonban igazságot tett a két császár között, egyetlen egyenes kardcsapással kettévágta a drágakövet! Ha a gyémánt egy konvex poliéder volt, melynek összesen 100 éle van, és egyetlen csúcsát sem vágta át, akkor legfeljebb hány élét metszhette ketté?
*Algebra (Azonosító: kk_2008_08f )
Az álnok Ebelasztin lovag akart kibabrálni Jánossal, amikor ezt a feladatot adta fel neki: Melyiklegnagyobb n pozitív egész, melyre $n\left(\sqrt{1000004}-\sqrt{1000001}\right) < 1$.
*Algebra ( másodfokú) (Azonosító: kk_2008_09f )
A magyar huszár sikerét irigyelve a gőgös Ebelasztin lovag is megpróbálkozott "Lucifer", a legvadabb császári mén betörésével, ám az csakhamar ledobta hátáról. A megszédült, kótyagos fejű lovagot ágyba fektették, és most éppen azt számolgatja, hogy a szemei előtt táncoló 50 különböző, $y=ax^2+bx+c$ alakú függvény grafikonja ($a\ne0$) hány részre osztja a koordinátasíkot. Ha helyesen számol, legfeljebb mennyit kaphatott eredményül?
*Kombinatorika (Azonosító: kk_2008_10f )
Háry egyszer igen díszes társaságban ebédelt, csupa hadvezérek között. Összesen hatan ültek a kör alakú asztalnál. Együtt összesen 120 csatát nyertek életük során. Mindegyikük pont annyiszor győzedelmeskedett, mint az óramutató irányában utána következő két vezér győzelmei számának különbségének abszolútértéke. Node a hadvezéreké hiú népség, így ha megkérdezzük őket, gyakran több győzelemről vallanak, mint amennyit arattak valójában, igaz, legfeljebb a valódi szám négyzetét hazudják. Legfeljebb hány győzelmet hazudhatnak így össze összesen?
*Számelmélet (Azonosító: kk_2008_11f )
Háry igazi gavallér, úgyhogy Mária Lujza születésnapjára annyi virágot vitt neki, ahány jegyű a 22008. Azonban Örzséjét jobban szerette, ő annyit kapott, ahány jegyű az $ 5^{2008}$. Hány szál virágot szedett összesen?
*Algebra (Azonosító: kk_2008_12f )
Háry tanácsára Ferenc császár rendkívüli hadikasszát nyit. Indulásként (a 0. év január elsején) egy jó nagy halom pénzt tesz bele. Innentől kezdve minden évben április 4-én reggel megduplázza az akkor benne levő összeget. Azonban az n. év nyarán a császár mind a 61 hadosztálya kap belőle 1000-szer n aranyat. A hadikincstár saját időszámítása adja meg n értékét, tehát az induló, 0. évben ennek megfelelően még nincs is kifizetés. Legalább hány ezer arannyal kell nyitnia a kasszát, ha azt akarja, hogy az sose ürülhessen ki teljesen?
*Algebra (Azonosító: kk_2008_13f )
A csata előtt Háry huszárjaival a következő játékot játssza: kisebb ágyúgolyókat tesznek 3 kupacba, egyikbe kettőt, a másikba négyet, a harmadikba nyolcat. János és ellenfele felváltva jön, a soron következő elveheti az egyik kupacból az abban levő golyóknak legalább a felét. Az nyer, aki az utolsó ágyúgolyót is elveszi. Háry persze azt állítja, hogy mindenkit meg tud verni, igaz, hozzáteszi, csak akkor, ha ő kezd. Ha igaza van, hányadik kupacból (x) kell elvennie és mennyit (y)? (A válaszlapra kerüljön x+3y értéke!)
*Geometria (Azonosító: kk_2008_14f )
A majlandi csatatér paralelogramma alakú, négy sarkánál egy-egy pózna áll, négy sarkát jelölje A, B, C, és D. Napóleon az AB oldalon áll, az E pontban, és a következők teljesülnek: AD=DE, DC=CE, CB=BE (ahol persze pl. AD az A és D póznák távolságát jelölik). Háry a B saroknál áll, mekkora szög alatt látja az AD oldalt?
*Geometria (Azonosító: kk_2008_15f )
A majlandi csatatér paralelogramma alakú, négy sarkánál egy-egy pózna áll, négy sarkát jelölje A, B, C, és D. Napóleon az AB oldalon áll, az E pontban, és a következők teljesülnek: AD=DE, DC=CE, CB=BE (ahol persze pl. AD az A és D póznák távolságát jelölik). Háry a B saroknál áll, mekkora szög alatt látja az AD oldalt?
*Számelmélet (Azonosító: kk_2008_16f )
Háry n huszárt vezet a majlandi csatába. Ha 10-esével osztja őket egy osztagba, akkor éppen eggyel több teljes létszámú csoportot tud kiállítani, mint ha 11-esével osztaná fel huszárjait. Hányféle lehet n? (n természetesen pozitív egész)
*Számelmélet (Azonosító: kk_2008_17f )
A majlandi csatában, ha Háry huszárait megszámoljuk, olyan számot kapunk, mely csak 0 és h számjegyeket tartalmaz, ugyanakkor Napóleon katonáinak száma meg csak 5 és h számjegyekből áll. Tudjuk még, hogy mindkét szám osztható 45-tel. Legalább hány katonát küldtek ketten együtt a csatába?
*Kombinatorika (Azonosító: kk_2008_18f )
A foglyul ejtett Napóleon alkut ajánl Hárynak: ha Háry képes megoldani Napóleon kedvenc, „repülő bástyás” sakkfeladványát, táviratot küld, melyben egész népét fegyverletételre szólítja fel. Ha azonban kudarcot vallana, köteles őt nyomban szabadon engedni. A feladvány így hangzik: „A repülő bástya úgy lép mint az igazi, csak éppen a szomszédos mezőre nem léphet, azt át kell „repülnie”. Indulj el a tábla sarkából , és járd be valamennyi mezőt, úgy, hogy visszatérsz ugyanebbe a sarokba , és minden más mezőt pontosan egyszer érintesz”- majd lerajzolt a földre egy k × k -as négyzet alakú táblát. Legalább mekkorának kell választani k értékét (k>1), hogy Háry elvégezhesse a fent leírtakat?
*Számelmélet (Azonosító: kk_2008_19f )
Amikor Háry hazatér Nagyabonyba, visz magával rokonainak a híres bécsi csokoládéból. 9 szelet jut összesen az n családtagjának. Hányféle lehet n (1-nél nagyobb pozitív egész), ha egyenlően szét tudja köztük osztani a csokoládékat úgy, hogy minden szeletet legfeljebb egyszer tör ketté?
*Számelmélet (Azonosító: kk_2008_20f )
20. „Was sagt er, bakter”; Háry elképedve mered Marci bácsira, az idős kocsisra, mert az imént azt állította, hogy ismeri az összes pozitív egész (m,n) számpárt, melyekre igaz, hogy:
$\dfrac{m}{n+1}<\sqrt{2}<\dfrac{m+1}{n}$
és m és n is kisebbek 1000-nél. Ha igazat beszél, hány megoldást jegyzett meg?


