1. találat: Matematika emelt szintű érettségi, 2011. október, II. rész, 5. feladat
Témakör: *Algebra (Azonosító: mme_201110_2r05f )
Írja fel annak az egyenesnek az egyenletét, amelyik illeszkedik a $ P(2; 5) $ pontra, valamint az $ x + y = 4 $ és az $ x + y = 6 $ egyenletű egyeneseket olyan pontokban metszi, amelyek első koordinátájának különbsége 3.
*Kombinatorika (Azonosító: mme_201110_2r06f )
a) Két szabályos dobókockát egyszerre feldobunk. Számítsa ki a következő két esemény valószínűségét: $ A $: a dobott pontok összege prím; $ B $: a dobott pontok összege osztható 3-mal.
b) Az 1, 2, 3, 4, 5, 6 számjegyekből véletlenszerűen kiválasztunk három különbözőt. Mennyi a valószínűsége annak, hogy a kiválasztott számjegyek mindegyikének egyszeri felhasználásával 4-gyel osztható háromjegyű számot tudunk képezni?
c) Az $ ABCD $ négyzet csúcsai: $A\left(0;0 \right),\ B\left(\dfrac{\pi} 2;0 \right),\ c\left(\dfrac{\pi} 2;\dfrac{\pi} 2 \right),\ D\left(0;\dfrac{\pi} 2 \right)$. Véletlenszerűen kiválasztjuk a négyzet egy belső pontját. Mennyi a valószínűsége annak, hogy a kiválasztott pont a koordinátatengelyek és az $ f:\left[0;\dfrac{\pi} 2 \right]\to\mathbb{R},\ f(x)=\cos x$ függvény grafikonja által határolt tartomány egyik pontja?
*Geometria (Azonosító: mme_201110_2r07f )
Egy pillepalack alakja olyan forgáshenger, amelynek alapköre 8 cm átmérőjű. A palack fedőkörén található a folyadék kiöntésére szolgáló szintén forgáshenger alakú nyílás. A két hengernek közös a tengelye. A kiöntő nyílás alapkörének átmérője 2 cm. A palack magassága a kiöntő nyílás nélkül 30 cm. A palack vízszintesen fekszik úgy, hogy annyi folyadék van benne, amennyi még éppen nem folyik ki a nyitott kiöntő nyíláson keresztül.
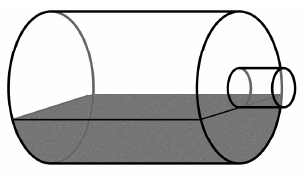
a) Hány deciliter folyadék van a palackban? (Válaszát egy tizedesjegyre kerekítve adja meg!)
A palack tartalmát kiöntve, a palackot összenyomva, annak eredeti térfogata 2p százalékkal csökken. Egy hulladékot újrahasznosító cég (speciális gép segítségével) az ilyen módon tömörített palack térfogatát annak további p százalékával tudja csökkenteni. Az összenyomással, majd az ezt követő gépi tömörítéssel azt érik el, hogy a palackot eredeti térfogatának 19,5 százalékára nyomják össze.
b) Határozza meg p értékét!
*Algebra (Azonosító: mme_201110_2r08f )
a) Ábrázolja a derékszögű koordináta-rendszerben az $ f : [0; 5]\to \mathbb{R}, f (x) = \left| x^2 - 4x + 3 \right| $ függvényt!
b) Tekintsük az $\left|(x-2)^2-1 \right|=k $ paraméteres egyenletet, ahol $ k $ valós paraméter. Vizsgálja a megoldások számát a $ k $ paraméter függvényében!
c) Ábrázolja a megoldások számát megadó függvényt a $ k \in ] - 6;6[ $ intervallumon!
d) Adja meg a c)-beli függvény értékkészletét!
*Kombinatorika (Azonosító: mme_201110_2r09f )
Öt, egymástól távol eső tanya között kábeleket feszítenek ki, bármely két tanya között legfeljebb egyet.
a) Elvileg összesen hány különböző hálózatot lehetséges létrehozni a tanyák között? (A hálózatban a kifeszített kábelek száma 0-tól 10-ig bármennyi lehet. Két hálózatot akkor tekintünk különbözőnek, ha van olyan összeköttetés, amely az egyikben létezik, de a másikban nem.)
b) Takarékossági okokból csak 4 kábelt feszítenek ki úgy, hogy a hálózat azért összefüggő legyen. (Összefüggőnek tekintünk egy hálózatot, ha a kábelek mentén bármely tanyáról bármely másikba el lehet jutni, esetleg más tanyák közbeiktatásával.) Hány különböző módon tehetik ezt meg, ha az egyes tanyákat megkülönböztetjük egymástól?


