1. találat: Matematika emelt szintű érettségi, 2014. október, II. rész, 5. feladat
Témakör: *Kombinatorika (átlag) (Azonosító: mme_201410_2r05f )
A tavaszi idény utolsó bajnoki mérkőzésén a Magas Fiúk Kosárlabda Klubjának (MAFKK) teljes csapatából heten léptek pályára. A mérkőzés után az edző elkészítette a hét játékos egyéni statisztikáját. Az alábbi táblázat mutatja a játékosok dobási kísérleteinek számát és az egyes játékosok dobószázalékát egészre kerekítve. (A dobószázalék megmutatja, hogy a dobási kísérleteknek hány százaléka volt sikeres.)
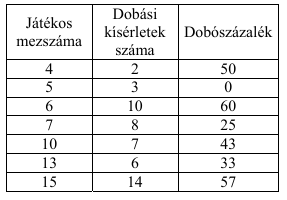
a) Számítsa ki, hogy mennyi volt a csapat dobószázaléka ezen a mérkőzésen!
Az őszi idény kezdete előtt egy hónappal a MAFKK csapatához csatlakozott egy 195 cm magas játékos, így a csapattagok magasságának átlaga a korábbi átlagnál 0,5 cm-rel nagyobb lett. Pár nap múlva egy 202 cm magas játékos is a csapat tagja lett, emiatt a csapattagok magasságának átlaga újabb 1 cm-rel nőtt.
b) Hány tagja volt a MAFKK-nak, és mekkora volt a játékosok magasságának átlaga a két új játékos csatlakozása előtt?
*Kombinatorika (geometria) (Azonosító: mme_201410_2r06f )
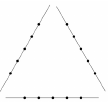
Megadtunk három egyenest, és mindegyiken megadtunk öt-öt pontot az ábra szerint.
a) Hány olyan szakasz van, amelynek mindkét végpontja az ábrán megadott 15 pont valamelyike, de a szakasz nem tartalmaz további pontot a megadott 15 pont közül?
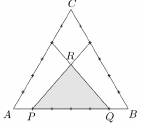
Az egyenlő oldalú ABC háromszög 18 egység hosszúságú oldalait hat-hat egyenlő részre osztottuk, és az ábra szerinti osztópontok összekötésével megrajzoltuk a PQR háromszöget.
b) Számítsa ki a PQR háromszög területének pontos értékét!
*Kombinatorika (geometria) (Azonosító: mme_201410_2r07f )
Egy üzemben egyforma, nagyméretű fémdobozok gyártását tervezik. A téglatest alakú doboz hálózatát egy 2 méter × 1 méteres téglalapból vágják ki az ábrán látható módon.
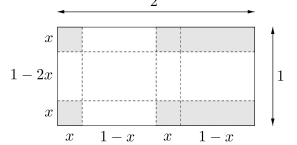
A kivágott idom felhajtott lapjait az élek mentén összeforrasztják. (A forrasztási eljárás nem jár anyagveszteséggel.)
a) Hogyan válasszák meg a doboz méreteit, hogy a térfogata maximális legyen? Válaszát centiméterben, egészre kerekítve adja meg!
A dobozokat egy öt karakterből álló kóddal jelölik meg. Minden kódban két számjegy és három nagybetű szerepel úgy, hogy a két számjegy nincs egymás mellett. Mindkét számjegy eleme a {0; 1; 2; 3; 4; 5; 6; 7; 8; 9} halmaznak, a betű ket pedig a 26 betűs (angol) ábécéből választják ki (például 7WA3A egy lehetséges kód).
b) Hány különböző kód lehetséges?
*Kombinatorika (logika, gráfelmélet) (Azonosító: mme_201410_2r08f )
a) Határozza meg az alábbi kijelentés ek logikai értékét (igaz-hamis)! Válaszait indokolja!
I. Van olyan hatpontú fagráf, amelyn ek minden csúcsa páratlan fokszámú.
II. Ha egy hétpontú egyszerű gráfnak 15 éle van, akkor a gráf összefüggő .
III. Van olyan fagráf, amelyben a csúcsok számának és az élek számának összege páros.
Egy hatfős társaság tagjai A , B , C , D , E és F . Mindenkit megkérdeztünk, hogy hány ismerőse van a többiek között (az ismeretség kölcsönös). A válaszként kapott hat természetes szám szorzata 180. Az is kiderült, hogy A-nak legalább annyi ismerőse van, mint B-nek, B-nek legalább annyi ismerőse van, mint C-nek, és így tovább, E-nek legalább annyi ismerőse van, mint F-nek.
b) Szemléltesse egy-egy gráffal a lehetséges ismeretségi rendszereke
*Algebra (kombinatorika, számtani sorozat) (Azonosító: mme_201410_2r09f )
Éva egy 7 × 7-es táblázat bal felső mezőjétől kezdve, balról jobbra haladva, sorról sorra beírta egy számtani sorozat első 49 tagját úgy, hogy a tagok sorrendjét nem változtatta meg. (A sorozat 1. tagja a bal felső sarokba került, a 8. tag a második sor első mezőjébe, a 49. tag pedig a jobb alsó sarokban áll.)
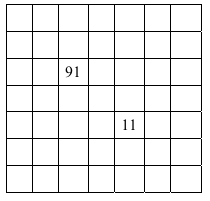
a) Mennyi a táblázatba írt 49 szám összege, ha Éva a harmadik sor harmadik mez ő jébe a 91-et, az ötödik sor ötödik mezőjébe pedig a 11-et írta?
Péter a táblázat minden sorából kiválasztja a számtani sorozat egy-egy tagját úgy, hogy a hét kiválasztott szám közül semelyik kettő ne legyen egy oszlopban.
b) Igazolja, hogy akárhogyan is választja ki Péter így a számokat, a hét szám összege minden esetben ugyanannyi lesz!
c) Határozza meg annak a valószínűségét, hogy a 91 és a 11 is a Péter által kiválasztott számok között lesz!


