1. találat: Matematika emelt szintű érettségi, 2016. május, II. rész, 5. feladat
Témakör: *Algebra (abszolútérték, gyökös, trigonometria) (Azonosító: mme_201605_2r05f )
Oldja meg a [4; 6] alaphalmazon az alábbi egyenleteket, illetve egyenlőtlenséget!
a) $ \left|5-\left|x\right|\right|=3$
b) $ \sqrt{2x-3}=\sqrt{x+10}-1 $
c) $ 2\cos^2x+\cos x-1 \leq 0 $
*Kombinatorika (gráf, valószínűség, skatulyaelv, indirekt,) (Azonosító: mme_201605_2r06f )
a) Legyen G egy nyolcpontú egyszerű gráf, amelynek összesen 9 éle van. Igazolja, hogy G csúcsai között biztosan van olyan, amelynek a fokszáma legalább 3.
b) Az A, B, C, D, E, F, G, H pontok egy szabályos nyolcszög csúcsai. Megrajzoljuk a nyolcszög oldalait és átlóit. A megrajzolt szakaszok közül véletlenszerűen kiválasztunk négyet. Határozza meg annak a valószínűségét, hogy mind a négy kiválasztott szakasz az A csúcsból indul ki!
c) Nyolc sakkozó részére egyéni bajnokságot szerveznek. Hányféleképpen készíthető el az első forduló párosítása, ha ebben a fordulóban mindenki egy mérkőzést játszik? (Két párosítást különbözőnek tekintünk, ha az egyik tartalmaz olyan mérkőzést, amelyet a másik nem.)
*Függvények (algebra, integrál, összetett függvény,) (Azonosító: mme_201605_2r07f )
Adott az f, a g és a h függvény:
$ f:\mathbb{R}\rightarrow \mathbb{R}, f(x)=2^x-1 $;
$ g:\mathbb{R}\rightarrow \mathbb{R}, g(x)=3x+2 $
$ h:\mathbb{R}\rightarrow \mathbb{R}, h(x)=12-x^2 $
a) Legyen a k összetett függvény belső függvénye az f és külső függvénye a h (vagyis $ k(x)=h(f(x)) $ minden x valós szám esetén). Igazolja, hogy $ k(x)=11+2^{x+1}-4^x $ .
b) Oldja meg az $ f(g(x))<g(f(x)) $ egyenlőtlenséget a valós számok halmazán!
c) Mekkora a h és az $ x \mapsto -4 $; $ (x \in \mathbb{R}) $ függvények görbéi által közbezárt (korlátos) terület?
*Valószínűségszámítás (térgeometria, térfogatszámítás, húrtrapéz, hasonlóság) (Azonosító: mme_201605_2r08f )
Egy kisüzemi meggymagozó-adagoló gép 0,01 valószínűséggel nem távolítja el a magot a meggyből, mielőtt a meggyszemet az üvegbe teszi. A magozógépen áthaladt szemek közül 120-120 darab kerül egy-egy üvegbe.
a) Számítsa ki annak a valószínűségét, hogy egy kiválasztott üvegben legalább 2 darab magozatlan szem van!
A termelés során keletkezett hulladékot nagy méretű konténerbe gyűjtik, melyet minden nap végén kiürítenek és kitisztítanak. A konténer egyenes hasáb alakú. A hasáb magassága 2 m, alaplapja húrtrapéz, melynek méretei az 1. ábrán láthatók. A konténert vízszintes felületen, az 1,8 m × 2 m-es (téglalap alakú) lapjára állítva helyezik el (lásd a 2. ábrát).
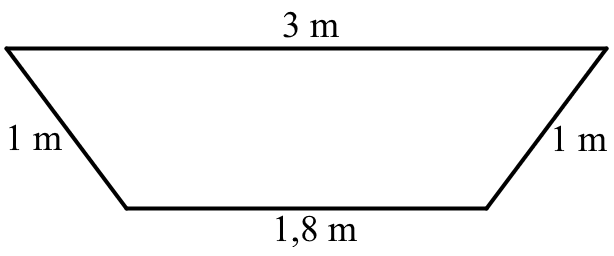 | 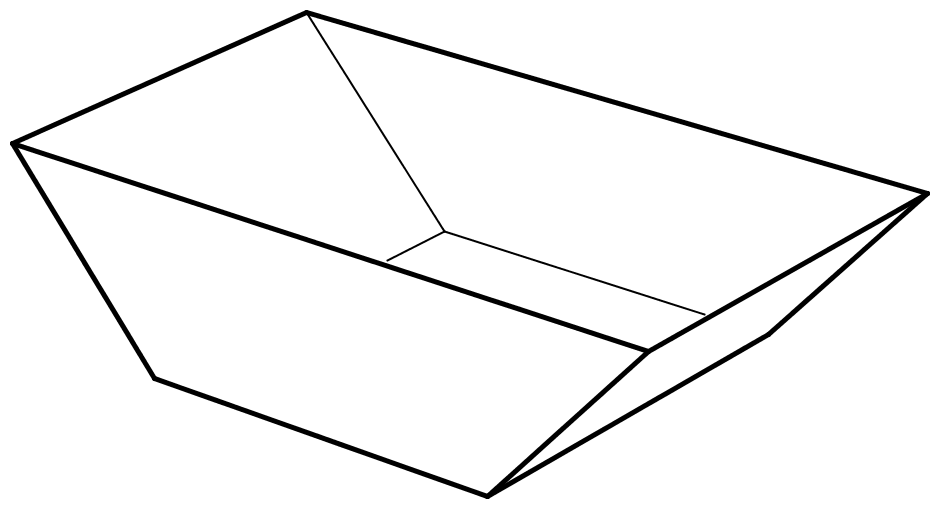 |
| 1. ábra | 2. ábra |
b) Számítsa ki a hasáb térfogatát! Határozza meg, hogy milyen magasan áll a konténerben a tisztításához beletöltött $ 2,7 m^3 $ térfogatú folyadék!
*Függvények (szélsőérték, differenciálszámítás, derivált, másodfokú függvény) (Azonosító: mme_201605_2r09f )
A repülőgépek üzemanyag-fogyasztását számos tényező befolyásolja. Egy leegyszerűsített matematikai modell szerint (a vizsgálatba bevont repülőgépek esetében) az egy óra repülés alatt felhasznált üzemanyag tömegét az $ f(x)=\dfrac{1}{20}(x^2-1800x+950\ 000) $ összefüggés adja meg. Ebben az összefüggésben x a repülési átlagsebesség km/h-ban (x > 0), f(x) pedig a felhasznált üzemanyag tömege kg-ban.
a) A modell alapján hány km/h átlagsebesség esetén lesz minimális az egy óra repülés alatt felhasznált üzemanyag tömege? Mekkora ez a tömeg?
Egy repülőgép Londonból New Yorkba repül. A repülési távolság 5580 km.
b) Igazolja, hogy v km/h átlagsebesség esetén a repülőgép üzemanyag-felhasználása ezen a távolságon (a modell szerint) $ 279v-502200+\dfrac{265\ 050\ 000}{v} $kg lesz! (v > 0)
A vizsgálatba bevont, Londontól New Yorkig közlekedő repülőgépek v átlagsebességére teljesül, hogy $ 800 km/h\leq v \leq 1100 km/h$.
c) A megadott tartományban melyik átlagsebesség esetén a legnagyobb, és melyik esetén a legkisebb az egy útra jutó üzemanyag-felhasználás?




