Egy háromszög oldalainak hossza 7 cm, 9 cm és 11 cm.

a) Igazolja, hogy a háromszög hegyesszögű!

Egy derékszögű háromszög oldalainak centiméterben mért hossza egy számtani sorozat három egymást követő tagja.

b) Igazolja, hogy a háromszög oldalainak aránya 3 : 4 : 5.

c) Ennek a derékszögű háromszögnek a területe $ 121,5\ cm^2 $. Számítsa ki a háromszög oldalainak hosszát!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

a) Határozza meg $ \dfrac{x}{y } $ értékét, ha $ \dfrac{2x+3y}{4c+2y}=\dfrac 9 {10};\ (y \ne 0, y\ne -2x) $.

b) Legyen $ f (x) = x^2-11x+30 $ . Igazolja, hogy ha $ f (x) \ne 0 $, akkor $\dfrac{f(x+1)}{f(x)}=\dfrac{x-4}{x-6} $ .

c) Oldja meg az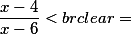

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Ágoston a tanév első két hónapjában három osztályzatot szerzett matematikából (osztályzatok: 1, 2, 3, 4 vagy 5). A második osztályzata nem volt rosszabb, mint az első, a harmadik osztályzata pedig nem volt rosszabb, mint a második.

a) Határozza meg a feltételeknek megfelelő lehetőségek (számhármasok) számát!

Ágoston osztálya kétnapos kirándulásra indul. Kulcsosházban szállnak meg egy éjszakára. A tanulók szállásdíja a résztvevők számától független, rögzített összeg. Az egy tanulóra jutó szállásköltség egy hiányzó esetén 120 Ft-tal, két hiányzó esetén pedig 250 Ft-tal lenne több, mint ha az egész osztály részt venne a kiránduláson.

b) Határozza meg az osztály létszámát és a teljes fizetendő szállásdíjat!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy adatsokaság hét pozitív egész számból áll. Az adatsokaságnak két módusza van, a 71 és a 75. Az adatsokaság mediánja 72, az átlaga 73, a terjedelme pedig 7.

a) Határozza meg a hét számot!

A 72-nek és az n pozitív egész számnak a legkisebb közös többszöröse 27 720.

b) Határozza meg az n lehetséges értékeinek számát, és adja meg az n legkisebb lehetséges értékét!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba