Az $ \left\{a_n \right\}$ számtani sorozat első és harmadik tagjának összege 26, a második és negyedik tagjának összege pedig 130.
a) Adja meg a sorozat ötödik tagját!
A $ \left\{ b_n \right\} $ mértani sorozat első és harmadik tagjának összege 26, a második és negyedik tagjának összege pedig 130.
b) Adja meg a sorozat ötödik tagját!
Marci szeret az autók rendszámában különböző matematikai összefüggéseket felfedezni. (A rendszámok Magyarországon három betűből és az azokat követő három számjegyből állnak.)
Az egyik általa kedvelt típusnak a "prímes" nevet adta: az ilyen rendszámoknál a PRM betűket követő három számjegy szorzata prímszám.
 a) Hány különböző "prímes" rendszám készíthető?
a) Hány különböző "prímes" rendszám készíthető?
Egy másik típusnak a "hatos" nevet adta: az ilyen rendszámokban a HAT betűket követő három számjegy összege 6.
 b) Hány különböző "hatos" rendszám készíthető?
b) Hány különböző "hatos" rendszám készíthető?
Egy harmadik típus a "logaritmusos". Ezek általános alakja: LOG-abc, ahol az a, b és c számjegyekre (ebben a sorrendben) teljesül, hogy $ \log_a b = c $.
 c) Hány különböző "logaritmusos" rendszám készíthető?
c) Hány különböző "logaritmusos" rendszám készíthető?
A mellékelt ábrán egy kereszt alakú lemez látható, amely 5 db 10 cm oldalú négyzetből áll. A lemezből egy 10 cm alapélű, szabályos négyoldalú gúla hálóját szeretnénk kivágni úgy, hogy a középső négyzet legyen a gúla alaplapja.
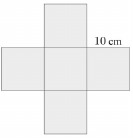
a) Igazolja, hogy a lehetséges hálók kivágása során keletkező hulladék legalább $ 200 cm^2 $, de kevesebb $ 300 cm^2 $-nél!
Tekintsük az ábrán látható nyolcpontú gráfot.
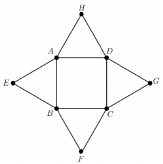
b) A gráfban véletlenszerűen kiválasztunk két csúcsot. Mennyi a valószínűsége annak, hogy a két csúcsot él köti össze a gráfban?
c) A gráf 9 élét kékre, 3 élét pedig zöldre színezzük. Igazolja, hogy bármelyik ilyen színezésnél lesz a gráfban egyszínű (gráfelméleti) kör!
Adott az $ x^2 - (4 p + 1) x + 2 p = 0 $ másodfokú egyenlet, ahol $ p $ valós paraméter.
a) Igazolja, hogy bármely valós $ p $ érték esetén az egyenletnek két különböző valós gyöke van!
b) Ha az egyenlet egyik gyöke 3, akkor mennyi a másik gyöke?
c) Határozza meg a $ p $ paraméter értékét úgy, hogy az egyenlet gyökeinek négyzetöszszege 7 legyen!


