Látogatók
Összes: 6 040 552 Mai: 4 079
|
1. találat: Matematika emelt szintű érettségi, 2020. május II. rész, 5. feladat
Témakör: *Algebra (Azonosító: mme_202005_2r05f )
Az északi félteke 50. szélességi körén egy adott napon a nappal hosszát (a napkelte és a napnyugta között eltelt időt) jó közelítéssel a következő f függvénnyel lehet modellezni: $ f(n)= -5,2\cos\left( \right)\dfrac{n+8}{58 }+11,2 $ ahol $ n $ az adott nap sorszámát jelöli egy adott éven belül, $ f(n) $ pedig a nappal hossza órában számolva $ (1 \le n \le 365 $, $ n \in \mathbb{N} )$.
Az alábbi ábra a $ g : [ 1;365 ] \rightarrow \mathbb{R}$; $g ( x) = -5,2\cos\left( \right)\dfrac{n+8}{58 }+11,2 $függvényt szemlélteti. (A $ g $ függvény az $ f $-nek egy folytonos kiterjesztése.) 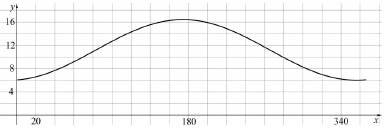
a) Ha $ x = 1 $, akkor $ \dfrac{x+8}{58} $ helyettesítési értéke $ \dfrac{9}{58} $. Adja meg a $ \dfrac{9}{58} $ radián értékét fokban mérve!
b) Számítsa ki a modell alapján, hogy az év 50. napján milyen hosszú a nappal! Válaszát óra:perc formátumban, egész percre kerekítve adja meg!
c) Igazolja, hogy (a modell szerint) egy évben 164 olyan nappal van, amelyik 12 óránál hosszabb!
Adott egy másik, az $ y = -5,2 \cos(x) + 11,2 $ egyenletű görbe, valamint az $ x = 0 $, az $ y = 0 $ és az $ x = 2\pi $ egyenletű egyenesek.
d) Számítsa ki a görbe és a három egyenes által határolt korlátos síkidom területét!
*Számelmélet (Azonosító: mme_202005_2r06f )
a) Hány olyan 90-nél nem nagyobb pozitív egész szám van, amely a 2, a 3 és az 5 közül pontosan az egyikkel osztható?
Az ötöslottó-játékban az első 90 pozitív egész számból kell öt különbözőt megjelölni. A sorsoláson öt (különböző) nyerőszámot húznak ki. (Sem a megjelölés, sem a kihúzás sorrendje nem számít.) Kati a 7, 9, 14, 64, 68 számokat jelölte meg. A sorsoláson az első három kihúzott nyerőszám a 7, a 9 és a 14 volt. Kati úgy gondolja, hogy most nagy esélye van legalább négy találatot elérni.
b) Határozza meg annak a valószínűségét, hogy a hátralevő két nyerőszám közül Kati legalább az egyiket eltalálja!
Az egyik játékhéten összesen 3 222 831 lottószelvényt küldtek játékba a játékosok. Az alábbi táblázat mutatja a nyertes szelvények számát és nyereményét (2-nél kevesebb találattal nem lehet nyerni). 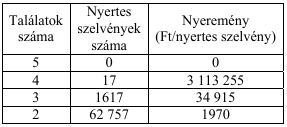
c) Számítsa ki, hogy mennyi volt a játékosok egy lottószelvényre jutó átlagos vesztesége ezen a héten, ha a játékba küldött szelvények egységára 250 Ft!
*Geometria (Azonosító: mme_202005_2r07f )
Az $ ABCD $ húrnégyszögben $ AB = 20 $, $ BC = 18 $, $ ABC\sphericalangle = 70^\circ $, $ CAD\sphericalangle = 50^\circ $.
a) Milyen hosszú a $ CD $ oldal, és mekkora a húrnégyszög területe?
A derékszögű koordináta-rendszerben adottak a $ P(-2; 0) $, $ Q(6; 0) $ és $ R(0; 5) $ pontok, a $ H $ pedig a $ PQ $ szakasz tetszőleges pontja.
b) Számítsa ki a $ \overrightarrow{PH} $ és az $ \overrightarrow{RH} $ vektorok skaláris szorzatát, ha $ H(-1,8; 0) $.
c) Adja meg a $ H $ pont koordinátáit úgy, hogy a $ \overrightarrow{PH} $ és az $ \overrightarrow{RH} $ vektorok skaláris szorzata maximális, illetve úgy is, hogy minimális legyen!
*Kombinatorika (Azonosító: mme_202005_2r08f )
Egy étteremben (hatósági engedély birtokában) az érvényes általános forgalmi adótól (áfa) kismértékben eltérő adókulcsok alkalmazásának hatását vizsgálták az ételek és italok fogyasztására nézve. Az ételek esetében 4%, az italok esetében 30% áfát adtak hozzá a nettó árhoz, és az így kapott bruttó árat kellett a vendégnek kifizetnie. A kísérlet első napján az új számítógépes program hibája miatt a számlán éppen fordítva adták a nettó árakhoz az áfát: az ételek nettó árához 30%-ot, az italok nettó árához pedig 4%-ot számoltak hozzá, és ez a számlán is így, hibásan jelent meg. Egy család ebben a vendéglőben ebédelt, és a hibás program miatt 8710 Ft-os számlát kapott. A hibát észrevették, így végül a helyes összeget, 7670 Ft-ot kellett kifizetniük.
a) Hány forint volt az elfogyasztott ételek, és hány forint volt az elfogyasztott italok helyes bruttó ára?
Egy másik étteremben 12 és 14 óra között 3900 Ft befizetéséért annyit eszik és iszik a vendég, amennyit szeretne. A befizetendő összeget egy előzetes felmérés alapján állapították meg. A felmérés során minden vendég esetén összeadták az elfogyasztott étel és ital árát az adott fogyasztáshoz tartozó összes egyéb költséggel. Az összesített költségek alapján osztályokba sorolták a vendégeket aszerint, hogy az étteremnek hány forintjába kerültek. Az alábbi táblázat mutatja a felmérés eredményét. A táblázat első sorában az osztályközepek láthatók. 
b) A felmérés eredményét felhasználva számítsa ki, hogy ennek az étteremnek 1000 vendég esetén mekkora a várható haszna!
c) A fenti táblázat értékeivel számolva mennyi a valószínűsége, hogy két (ebédre betérő) vendég együttes fogyasztása veszteséget jelent az étteremnek? (A táblázatba foglalt információkat tekinthetjük úgy, hogy egy véletlenszerűen betérő vendég esetén pl. 0,25 annak a valószínűsége, hogy a vendég 2800 Ft-ba kerül az étteremnek.)
*Kombinatorika (Azonosító: mme_202005_2r09f )
Egy városban a közösségi közlekedést kizárólag vonaljeggyel lehet igénybe venni, minden utazáshoz egy vonaljegyet kell váltani. A vonaljegy ára jelenleg 300 tallér. Az utazások száma naponta átlagosan 100 ezer. Ismert az is, hogy ennek kb. 10%-ában nem váltanak jegyet (bliccelnek).
A városi közlekedési társaság vezetői hatástanulmányt készíttettek a vonaljegy árának esetleges megváltoztatásáról. A vonaljegy árát 5 talléronként lehet emelni vagy csökkenteni. A hatástanulmány szerint a vonaljegy árának 5 talléros emelése várhatóan 1000-rel csökkenti a napi utazások számát, és 1 százalékponttal növeli a jegy nélküli utazások (bliccelések) arányát. (Tehát például 310 talléros jegyár esetén naponta 98 000 utazás lenne, és ennek 12%-a lenne bliccelés.) Ugyanez fordítva is igaz: a vonaljegy árának minden 5 talléros csökkentése 1000-rel növelné a napi utazások számát, és 1 százalékponttal csökkentené a bliccelések arányát. A tanulmány az alkalmazott modellben csak a 245 tallérnál drágább, de 455 tallérnál olcsóbb lehetséges jegyárakat vizsgálta.
a) Mekkora lenne a közlekedési társaság vonaljegyekből származó napi bevétele a hatástanulmány becslései alapján, ha 350 tallérra emelnék a vonaljegyek árát?
b) Hány talléros vonaljegy esetén lenne maximális a napi bevétel?
|
|


