Látogatók
Összes: 6 021 159 Mai: 4 012
|
1. találat: Matematika emelt szintű érettségi, 2021. május II. rész, 5. feladat
Témakör: *Algebra (Azonosító: mme_202105_2r05f )
a) Határozza meg az $ m $ valós szám összes lehetséges értékét úgy, hogy az alábbi kijelentés igaz legyen! Az $ x^ 2 − 2 x + 4 = mx $ egyenletnek pontosan két különböző valós gyöke van. b) Mutassa meg, hogy az alábbi kijelentés igaz! Az $ f\ :\ \mathbb{R} \rightarrow \mathbb{R};\ f ( x) = \dfrac{3}{(1+\cos x)^2+2} $ függvény értékkészlete az $ \left[\dfrac{1}{2};\dfrac{3}{2} \right] $ intervallum.
c) Tudjuk, hogy az $ A $,$ B $,$ C $ kijelentések mindegyike$ 0,6 $ valószínűséggel igaz és$ 0,4 $ valószínűséggel hamis. Ebben az esetben mennyi annak a valószínűsége, hogy az $ (A ∧ B) ∨ C $ kijelentés igaz?
*Algebra (Azonosító: mme_202105_2r06f )
Egy nyomozás során fontossá vált felderíteni azt, hogy az $ A$, $ B $, $ C $, $ D $, $ E $, $ F $ hattagú társaság mely tagjai ismerik egymást, azaz milyen a társaság ismeretségi hálója (ismeretségi gráfja). (Az ismeretség bármely két tag között kölcsönös. A társaság két ismeretségi hálója akkor különböző, ha van két olyan tag, akik az egyik hálóban egymásnak ismerősei, de a másikban nem.) A nyomozás során az már bizonyítottá vált, hogy $ A $-nak 5, $ B $-nek 4, $ C $-nek 3 ismerőse van a társaságban. Ennél többet azonban nem sikerült kideríteni, így aztán $ D $, $ E $ és $ F $ egymás közötti ismeretségeiről sincs még semmilyen információ.
a) Hányféle lehet a $ D $, $ E $, $ F $ csoport ismeretségi hálója?
A friss bizonyítékok szerint a $ D $, $ E $, $ F $ csoportban mindenki ismeri a másik két személyt.
b) Az összes eddigi (a korábban és a frissen beszerzett) információt figyelembe véve hányféle lehet az$ A$, $ B $, $ C $, $ D $, $ E $, $ F $ hattagú társaság ismeretségi hálója?
A további információk kiderítése érdekében a hattagú társaság tagjait 3 fős csoportokba szervezve hallgatják ki. Minden olyan 3 fős csoport kihallgatását megszervezik, amelyben $ A $ és $ B $ együtt nincs jelen.
c) Összesen hány ilyen csoportos kihallgatást kell szervezni?
*Algebra (Azonosító: mme_202105_2r07f )
Egy nyolcfős csapat kosárlabdaedzése közben mind a nyolcan 10-szer kíséreltek meg hárompontost dobni. A sikeres dobások számát mind a nyolc főnél felírták. A feljegyzett számok: 6, 3, 7, 6, 4, 7, 8 és 7.
a) Határozza meg a sikeres dobások számának átlagát, mediánját és szórását!
A kosárlabda büntetődobást 4,6 méter távolságról kell elvégezni, a gyűrű 3 méter magasan van. Petra a dobás pillanatában 2 méter magasságból engedi el a labdát, és az ideális, vízszintessel bezárt $ 45^\circ $-os szögre törekszik a dobás indításánál.
b) Petra dobásának modellezéséhez határozza meg annak a parabolának az egyenletét, amely áthalad a $ P(0; 2) $ és a $ Q(4,6; 3) $ ponton, a $ P $ pontban húzott érintőjének irányszöge pedig $ 45^\circ $! A parabola egyenletét $ y = ax^ 2 + bx + c $ alakban adja meg! 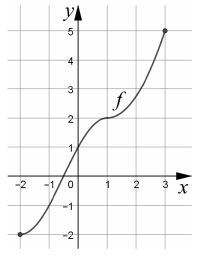
Az ábrán a $ [-2; 3] $ intervallumon értelmezett szigorúan monoton, folytonos $ f $ függvény grafikonja látható.
c) Adja meg az $ f $ inverzfüggvényének értelmezési tartományát, értékkészletét, zérushelyét, és jellemezze az inverzfüggvényt monotonitás szempontjából!
*Algebra (Azonosító: mme_202105_2r08f )
Egy sorsjegyből jelenleg havonta átlagosan 5000 darabot értékesítenek. Egy darab sorsjegy ára 500 Ft, de a forgalmazó cég ezt csökkenteni szeretné. A sorsjegy ára 10 Ft-os lépésekben csökkenthető. Azt feltételezik, hogy ha az ár $ n $-szer 10 Ft-tal alacsonyabb lesz, akkor havonta $ 10n^2 $-tel több sorsjegyet tudnak eladni ($ n \in \mathbb{N}^+ $). Tekintsük ezt a feltételezést helytállónak.
a) Határozza meg a sorsjegyek eladásából származó havi bevételt, ha a sorsjegy árát 300 Ft-ra csökkentik!
b) Határozza meg azt az n értéket, amelyre a sorsjegyek eladásából származó havi bevétel maximális lenne!
Az összes sorsjegy 5%-a nyerő. Kétféle nyeremény van: 2500 Ft-os és 50 000 Ft-os. A 2500 Ft-os nyerő sorsjegyből pontosan 24-szer annyi van, mint az 50 000 Ft-osból.
c)Töltse ki az alábbi táblázat üres mezőit, majd számítsa ki egy darab sorsjegy nyereményének várható értékét! 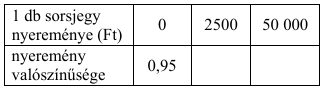
*Algebra (Azonosító: mme_202105_2r09f )
Egy teherautó raktere 2,4 méter széles, 2 méter magas és 7 méter hosszú. Ezzel a teherautóval kell olyan, méretre vágott farönköket szállítani, amelyek forgáshenger alakúak, 24 centiméter az átmérőjük, és 7 méter hosszúak. A rakomány biztonsági okokból nem nyúlhat túl a raktéren egyik irányban sem. A szállítócég az ábrán látható stratégiával rendezi el a farönköket. 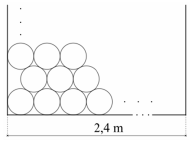 a) Mutassa meg, hogy legfeljebb 86 farönköt lehet így a raktérben elhelyezni! a) Mutassa meg, hogy legfeljebb 86 farönköt lehet így a raktérben elhelyezni!
b) A raktérnek hány százaléka marad üresen, ha 86 farönköt szállítanak?
Kiderült, hogy a fák egy részében megtelepedtek a szúbogarak. Bármelyik fát kiválasztva 4% annak a valószínűsége, hogy van benne szú. Az egyik vásárló cég 50 fát vett.
c) Mennyi a valószínűsége, hogy legfeljebb egy szúrágta fa kerül a rakományába?
|
|


