Árki Tamás és Hraskó András

Kísérletező geometria

Készült a Közoktatási Modernizációs Közalapítvány (KOMA) támogatásával

Árki Tamás

Dinamikus geometriai rendszerek jellemzői

A Cabri geometria gondolatának születése az 1980-as évekre vezethető vissza, amikor is a Joseph Fourier Egyetem (Franciaország, Grenoble) kutatócsoportja Jean-Marie Laborde vezetésével megfogalmazta egy, a geometria tanítását segítő számítógépes környezet fejlesztésének célkitűzéseit. A fejlesztés gyorsan el is indult, amelynek eredményeként 1987-re megszületett a Cabri első, iskolások által már kipróbálható verziója. A program gyors sikerét mi sem bizonyítja jobban, minthogy 1988-ban már az év oktatóprogramjának választották Franciaországban.

A Cabri elnevezés betűszót takar, amely a nem könnyen kiolvasható CAhier de BRouillon Interactif (pour l’apprentissage de la géometrie) kifejezésből származik, és magyarra interaktív geometriai jegyzetként fordítható.

A program Cabri II változata 1994-ben jelent meg, és 1998-ra készült el a Windows alatt futó változata. A jelenlegi legfrissebb változat, amely 2003-ban jelent meg, a Cabri II+ verziószámot viseli. Az első magyar változat 1994-ben jelent meg, Miklós Dezső fordításában.

Röviden tekintsük át a Cabri geometria filozófiáját, célkitűzéseit. A Cabri programmal új szoftvercsalád született, amelynek programjai a Dinamikus Geometriai Szerkesztőprogramok (Dynamic Geometry Software, DGS) nevet kapták. Egy ilyen program a következő feltételeknek mindenképpen megfelel:

Interaktív adatkezelés

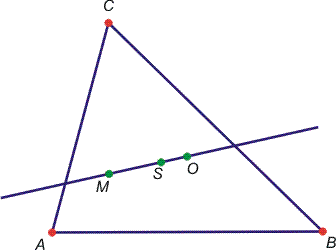
A geometriai szerkesztések pontokra épülnek fel. A pontok kétfélék lehetnek; bázispontok, amelyeket a szerkesztés elején önkényesen helyezünk el a rajzlapon, illetve származtatott pontok, amelyeket különféle szerkesztések eredményeként kapunk meg. Az ilyen pontok helyét a bázispontok határozzák meg. Az interaktív adatkezelés lényege az, hogy a bázispontokat szabadon megfoghatjuk az egérrel, és arrébb vihetjük, míg a származtatott pontok, és egyéb alakzatok követik a bázispontok helyzetét, biztosítva, hogy az elemek közötti logikai kapcsolatok a mozgatás során nem sérülnek. Példaként az dgs001_01. ábrán pirossal jelöltük a szabadon mozgatható bázispontokat (A, B, C), zölddel a származtatott pontokat (M magasságpont, S súlypont, O körülírt kör középpontja), kékkel a további származtatott objektumokat. A bázispontok mozgatásával meggyőződhetünk arról, hogy az említett nevezetes pontok a bázispontok különböző helyzetei mellett is egy egyenesre illeszkednek.

dgs001_01. ábra. A kép