| A(z) para001 kódszámú óra | 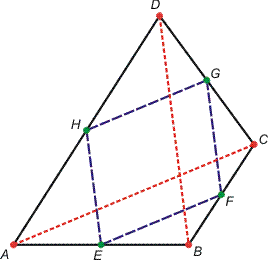 |
| Javasolt évfolyam: | 9-10. |
| Segédeszköz: | Gépterem, számítógépek, kivetítő, |
| Következő óra: | para002 óra |
Feladatok
para001 feladatTükrözzük a háromszög egy tetszőleges belső pontját a
háromszög oldalfelező pontjaira! Figyeljük meg a tükörképeket! Keressünk
kapcsolatot az eredeti, valamint a tükörképek alkotta háromszögek között! Fogalmazzuk meg sejtésünket!
para002 feladatSzerkesszük meg az adott konvex négyszög oldalfelező
pontjait! Milyen tulajdonságai vannak az így keletkező négyszögnek? Milyen
tulajdonságú négyszögből kell kiindulnunk ahhoz, hogy az oldalfelező pontok
alkotta négyszög téglalap legyen? Változtassuk a négyszög csúcsait, és
vizsgáljunk meg konkáv négyszögeket is!
para005 feladatAz ABCD paralelogramma BC oldalának
felezőpontja E, CD oldalának felezőpontja F. A DE
egyenes, valamint az AB egyenes metszéspontját jelölje G, míg a BF
egyenes és az AD egyenes metszéspontját H. Legyen végül I
a DG és BH egyenesek metszéspontja!
Vizsgáljuk meg a szerkesztést a bázispontok mozgatása mellett!
a) Milyen kapcsolatot találunk a H, C, G
pontok között?
b) Milyen kapcsolatot találunk az A, I, C
pontok között?
c) Számítsuk ki az IE/EG arányt! Mit
tapasztalunk?
Fogalmazzuk meg sejtéseinket!
Előzetes megjegyzés, segítség, megoldás és folytatási javaslat kérése
Házi feladatok
para003 feladatAdott az
ABCD konvex négyszög, és belsejében a
P
pont. Szerkesszük meg az
ABP,
BCP,
CDP,
DAP
háromszögek súlypontját, valamint a súlypontok alkotta négyszöget! Vizsgáljuk
meg, hogy a
P pont helyzetétől függően milyen tulajdonságokkal
rendelkezik a kapott négyszög? Fogalmazzuk meg sejtéseinket!
para004 feladatLegyen az adott
ABCD konvex négyszög átlóinak
metszéspontja
O. Szerkesszük meg az
OAB,
OBC,
OCD,
ODA
háromszögek köré írt körök középpontját! Milyen tulajdonságokkal rendelkezik a
középpontok alkotta négyszög? Milyen feltételek mellett lesz e négyszög téglalap?
Előzetes megjegyzés, segítség, megoldás és folytatási javaslat kérése
