A 2002-2003 tanévi 11-12-es FPI tehetséggondozó szakkör 17. foglalkozása
Kódok
Összeállította Hraskó András és Szőnyi Tamás
3. szakkör
A szakkörön mégsem a Kömal példák kerültek terítékre, hanem tovább folytattuk a Kódok feladatgyűjtemény
feldolgozását. Egy bemelegítő feladat után tisztáztuk az ISBN szám felépítését
(4.2), majd 1-hiba javító kódot gyártottunk (4.6) és totóztunk is
(5.6, 5.7). Menet közben megismerkedtünk a Hamming távolság
fogalmával, és néhány egyszerű lemmát fogalmaztunk meg a kódok minimális
távolsága és hibajelző, illetve javító képessége között (péládul 4.5).
Házi feladat lesz: 5.9, és egy szokatlan példa a 7-szög bináris mintáiról.
Négyzetminta
Egy négyzet csúcsaiba egy-egy egész
számot írtunk, majd mindegyik csúcs mellé még odaírtuk az abba a csúcsba írt
számnak a szomszédos csúcsokba írt számokkal vett összegét. Hány páratlan szám
lehet az így kapott nyolc szám között? Adjuk meg az összes lehetőséget!
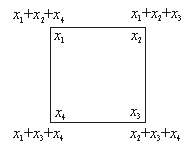
Megoldás
A feladat nem nehéz, 0, 4 vagy 8 páratlan számot kaphatunk.
Ez az egyszerű példa a későbbiekben egészen más összefüggésben elő fog bukkanni, az lesz
az igazi feladat, hogy észrevegyük, mikor.
3.2
Nézzük meg sok különböző könyv
azonosítóját, az úgynevezett ISBN (International Standard Book Number) számot!
Próbáljuk meg kideríteni, milyen részekből áll, hogyan épül fel ez az
azonosító! (Segítség: a legutolsó jegy egy ellenőrző jegy, segítségével
kiszűrhető bármelyik két számjegy felcserélése, illetve bármelyik jegy elírása.
A többi jegy három csoportba osztható és a könyv azonosítására szolgál.)
Megoldás
Nagy segítséget jelent, ha észrevesszük, hogy néhány ISBN számban az utolsó jegy nem
is szám, hanem az X jel. Innen sejthető, hogy az ellenőrző jegy a múlt órai 4.1
feladat megoldásához hasonlóan adható meg, csak annyi a különbség, hogy
mod 11 kell számolni.
A Bergengóc példatár első kiadásának kódja pld ISBN 963 9132 31 4. Ebből az első három
jegy, 963, Magyarország kódja. Nagyobb országoknak kevesebb jegyből áll a
kódja, hogy több maradjon a könyv azonosítására. A következő négy jegy, 9132, a
Typotex kiadót jelöli. Ez egy viszonylag kis kiadó, ezért ilyen hosszú a kódja.
A következő két szám, a 32, a könyv sorszáma. Ha a Typotex túllépi a kódjához
tartozó 100 könyv kiadására lehetőséget adó keretet, akkor majd új kódot kap.
Az utolsó jegy, a 4-es az ellenőrző jegy, ez a korábbiakból így számítható ki:
4 ≡ 1·9 + 2·6 + 3·3 + 4·9 + 5·1 + 6·3 + 7·2
+ 8·3 + 9·1 (mod 11).
Ha a szorzatösszeg 11-es maradéka 10 lenne, akkor az X betű lenne az ellenőrző jegy.
Általánosabban: az ISBN kód első kilenc jele egy-egy számjegy, ezek az országot, azon belül a
kiadót, illetve a könyvet azonosítják; ezen belül nincs rögzítve, hogy e három
jellemző melyike hány helyen tárolódik; nagyobb országok, nagyobb kiadók
rövidebb, kisebb országok, kisebb kiadók hosszabb karaktersort kapnak; összesen
mindig 9 jegyből áll ez a három rész. A tizedik jegy meghatározására az alábbi
egymással ekvivalens feltételek bármelyike alkalmazható.
x10 ≡ 2·x9 + 3·x8 +
4·x7 + 5·x6 +
6·x5 + 7·x4 +
8·x3 + 9·x2 +
10·x1 (mod 11);
x10≡
1·x1 + 2·x2 +
3·x3 + 4·x4 +
5·x5 + 6·x6 +
7·x7 + 8·x8 +
9·x9 (mod 11);
0 ≡ 1·x10
+ 2·x9 + 3·x8 +
4·x7 + 5·x6 +
6·x5 + 7·x4 +
8·x3 + 9·x2 +
10·x1 (mod 11);
0 ≡ 1·x1 +
2·x2 + 3·x3 +
4·x4 + 5·x5 +
6·x6 + 7·x7 +
8·x8 + 9·x9 +
10·x10 (mod 11).
Az utolsó alakból könnyen leolvasható, hogy az ellenőrző jegy kiszűri bármely két jegy
cseréjét vagy bármelyik jegy elírását. Ha pld az ötödik jegyet
x5-ről
x5'-re módosítjuk, akkor nem állhat fenn a
0 ≡ 1·x1 +
2·x2 + 3·x3 +
4·x4 + 5·x5 +
6·x6 + 7·x7 +
8·x8 + 9·x9 +
10·x10 (mod 11),
0 ≡ 1·x1 +
2·x2 + 3·x3 +
4·x4 + 5·x5'
+ 6·x6 + 7·x7 +
8·x8 + 9·x9 +
10·x10 (mod 11)
közül mindkettő, mert különbségük:
0 ≡ 5·( x5 - x5')
(mod 11),
és mivel 11 prím, így ez csak akkor állhat fenn, ha
0 ≡ x5 - x5'
(mod 11),
azaz
x5 =
x5', tehát ha nem is történt módosítás. Ehhez hasonlóan, ha
feltételezzük, hogy az
i-edik és
j-edik jegy cseréje érvényes
számot eredményez, akkor a
0 ≡ (i - j)·(xi
- xj) (mod 11)
kongruenciához jutunk, amelyben |
i -
j | < 10 és |
xi -
xj
| < 10, tehát
i =
j vagy
xi =
xj
, azaz nem történt valódi csere.
Néhány további azonosító leírását is összegyűjtöttük.
Most következzék egyszerre két feladat:
5.6
Bergengóciában a totó, a bajnokságnak megfelelően csak 4 mérkőzést tartalmaz. Minden mérkőzés eredményére
háromféleképpen lehet tippelni: 1-gyel, 2-vel vagy X-szel. Egy
szelvényen csak egy tipposzlop van.
a) Hány szelvényt kell venni ahhoz, hogy
biztosan legyen telitalálatunk?
b) És ahhoz, hogy biztosan legyen olyan
szelvényünk, amely legalább 3 találatos?
Definíció (Hamming távolság)
Ha adott két szó (azaz két azonos hosszúságú jelsorozat), akkor sorban összehasonlíthatjuk a
bennük lévő jeleket:
először a két szó első jeleit vetjük össze, azután a szavakban másodiknak következő jeleket,
..., végül az utolsókat.
Azoknak a helyeknek a számát, ahol egymástól különböző jeleket találunk, a két szó
Hamming távolságának nevezzük.
Formálisan:
dH(x1x2x3...xn,
y1y2y3...yn)
= |{i| xi ≠ yi}|,
Pld
dH(
AABC,
ABBA) = 2, mert a második helyen (
A ill.
B) és a
negyediken (
C és
A) van eltérés.
Definíció (Kód minimális távolsága)
Egy adott kód minimális távolságán a különböző kódszavai között fellépő legkisebb Hamming
távolságot értjük.
Lemma
Egy kód pontosan
akkor 1-hiba javító, ha minimális távolsága legalább 3.
Bizonyítás
Ha a kód nem
1-hiba javító, akkor van olyan p kódszó (pld AABA), amit egy
betűjében megváltoztatva egy c1 kódszóhoz jutunk (pld AABC),
de meg lehet p-t úgy is változtatni egy betűvel, hogy egy c2
kódszót kapjunk (pld ABBA). Ebben az esetben a c1, c2
kódszavak Hamming távolsága egy vagy kettő attól függően, hogy a két esetben a
változtatás ugyanazon a helyen történt vagy nem. Tehát 1-hiba javításra
alkalmatlan kódok minimális távolsága kisebb 3-nál.
Másrészt, ha
egy kód minimális távolsága kisebb, mint 3, akkor van a kódban két olyan
kódszó, c1, c2 (pld AABC és ABBA),
amelyek Hamming távolsága 2 vagy 1. Ha a távolság 2, akkor könnyen készíthetünk
olyan p szót, amely mindkét kódszótól csak egy helyen tér el: p
egyezzen meg c1-gyel és c2-vel mindazokon a
helyeken, ahol c1 és c2 megegyezik
egymással (p = A_B_), az eltérést okozó két hely egyikén
pedig p egyezzen meg c1-gyel (p = AAB_,
vagy A_BC), a másikon c2-vel (p = AABA,
vagy p = ABBC). Ha véletlenül a p üzenet érkezik hozzánk,
akkor nem tudjuk kijavítani. Ha c1 és c2
Hamming távolsága csak 1, akkor c1-et kapva bizonytalanságban
vagyunk, hogy c1-et vagy c2-t küldték, ha
egy hibát megengedünk.
1. házi feladat: 4.11
Bizonyítsd be, hogy egy kód pontosan akkor
a) k-hiba javító, ha minimális
távolsága legalább 2k+1;
b) k-hiba jelző, ha minimális
távolsága legalább k+1;
c) k-törlés javító, ha k-hiba
jelző!
Most visszatérünk a 4.6 feladat megoldásához.
4.6 I. megoldása (A minimális távolság alapján)
Tegyük fel, hogy már van egy ilyen kódunk! Legyenek a betűk 0, 1, 2, és gyűjtsük össze a
0-val kezdődő kódszavakat! Legfeljebb három lehet belőlük, mert ha már négy
volna, akkor volna közöttük kettő, amelyek a második "betűben" is
megegyeznek, és így legfeljebb csak két helyen térnek el egymástól. Teljesen
hasonlóan az 1-gyel és a 2-vel kezdődő szavakból is legfeljebb három-három
lehet, tehát összesen legfeljebb csak 9 ilyen kódszó van.
Találtam is 9 megfelelő kódszót:
|
0
|
0
|
0
|
0
|
|
1
|
0
|
1
|
2
|
|
2
|
0
|
2
|
1
|
|
0
|
1
|
1
|
1
|
|
1
|
2
|
0
|
1
|
|
2
|
1
|
0
|
2
|
|
0
|
2
|
2
|
2
|
|
1
|
1
|
2
|
0
|
|
2
|
2
|
1
|
0
|
Először a
0-val kezdődőket írtam össze (első oszlop). Egyszerűnek tűnt a maradék három
jegyet mindig egyformának választani. Ezután már alig volt szabadságom. Kellett
még három-három 1-gyel és 2-vel kezdődő kódszó. Ezeknek az utolsó három helyén
0-ból, 1-ből és 2-ből is csak egy-egy fordulhatott elő szavanként, hogy a már
kijelölt három kódszó egyikével se egyezzenek meg két helyen. Három jelnek épp
hat permutációja van, ez adja az esélyt. Miután leírtam az 1021 kódszót is már
csak egyféleképpen lehetett folytatni: 021 ciklikus elforgatottjait kellett
leírni az 1-es mögé, hogy ne legyen újabb egyezés, a másik három permutációt
pedig a 2-es mögé.
4.6 II. megoldása (Algebrai
konstrukció az 1.1 feladat analógiájára)
Ha a kódszavakat 1-1 helyen az összes lehetséges módon megváltoztatjuk, akkor csupa
különböző szóhoz kell jutnunk. Egy kódszónak négy betűje van, mindegyiket
kétféleképpen változtathatjuk meg, így egy kódszóhoz önmagával együtt 9 szó
tartozik. Mivel összesen 34 = 81 szó van, így legfeljebb 81/9 = 9
kódszó lehetséges.
Megadunk 9 megfelelő kódszót. Legyen a négy betű sorban x1, x2,
x3 és x4. Válasszuk meg
x1-et és x2-t az összes lehetséges módon!
Ez összesen épp 9 lehetőség.
x3-at és x4 számítsuk ki x1-ből
és x2-ből az 1.1
feladat megoldása alapján, csak modulo 3 számolva:
x3 ≡
x1 + x2 (mod 3), x4
≡ x1 + 2·x2 (mod 3).
Tehát a
kódszavak: 0000, 0112, 0221, 1011, 1120, 1202, 2022, 2101, 2210.
Ha kapunk egy
négybetűs szót, akkor "betűit" helyettesítsük be a fenti
egyenletekbe. Ha mindkettő teljesül, akkor nincs hiba (vagy egy hibánál több
van). Ha csak az egyik nem teljesül, akkor annak bal oldala a hibás és
kijavítható. Ha egyik se teljesül, akkor x1 és x2
egyike a hibás, az első egyenletből kiderül mennyivel, a másodikból, hogy
melyik.
Megjegyzés:
Ha a II. megoldást úgy módosítjuk, hogy x3-at és x4-et
az
x3 ≡
x1 + x2 (mod 3), x4
≡ 2·x1 +
x2 (mod 3)
képletekkel értelmezzük, akkor épp az I. megoldásban kapott 9 kódszóhoz jutunk.
5.6 a) megoldása
34 = 81-féleképpen alakulhat a négy mérkőzés eredménye, ezért ennyi, azaz 81
szelvényt kell kitölteni a biztos telitalálat érdekében.
5.6 b) I. megoldása
Összesen 9-féleképpen lehet úgy kitölteni a totószelvényt, hogy legalább háromtalálatos
legyen:
van 1 négytalálatos;
van 2 olyan, amelyen az 1., a 2., és a 3. mérkőzésre adott tipp talált (a 4. mérkőzés
eredményre adott tipp kétféleképpen lehet rossz);
és még 2-2-2 olyan szelvény képzelhető el, amelyen az 1., 2., 4.; az 1., 3., 4.; illetve a
2., 3., 4. mérkőzés eredményét találtuk el.
Ezért csak 81-9=72 olyan kitöltés lehetséges, amely legfeljebb kéttalálatos. Tehát 73
szelvényt kell ahhoz venni, hogy biztosan legyen egy legalább háromtalálatos.
Megjegyzés:
Ez a megoldás hibás,
mert nem a feltett kérdésre válaszol, hanem a következőre: hány szelvényt kell
vennie a nagyon buta totózónak, ha azt akarja, hogy azokat gondolkodás nélkül,
de csupa különböző módon kitöltve legyen egy legalább háromtalálatos szelvénye.
Egy gondolkodó totózó kevesebb szelvénnyel is el tud érni három (vagy több)
találatot.
5.6 b) II. megoldása
Ha háromtalálatosat szeretnénk, a következőképpen járunk el. Mivel a negyedik tipp
nem számít, csak az első hármat nézzük. Ezeket 3·3·3-féleképpen
tölthetjük ki. Tehát bármilyen is a telitalálatos, biztos lesz a kitöltöttek között
háromtalálatos. Így 27 szelvényt kell ehhez kitölteni.
Megjegyzés:
Ez a megoldás is hibás, ugyanis nem derül ki belőle, hogy 27-nél kevesebb szelvénnyel nem
oldható meg a feladat (szerencse nélkül).
5.6 b) III. megoldása
A négy mérkőzés együttes eredményét röviden "eredmény"-nek fogjuk hívni.
Ha egy szelvényt kitöltünk, akkor 9 olyan eredmény van, amely mellett van három
találatunk: a telitalálat, valamint ha a 3 mérkőzés közül pontosan egynél
hibáztunk (2-féle hiba lehetséges): 1+4·2=9. Nem úszhatjuk meg tehát 81/9=9
szelvénynél kevesebbel. Nézzük meg, hogy 9 szelvénnyel boldogulhatunk-e!
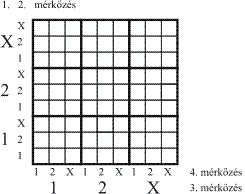
A szelvények mindegyike 9 eredmény esetén nyer (azaz 3 vagy 4 találatos). Ahhoz,
hogy mind a 81 lehetséges eredmény esetén legyen nyerő szelvényünk az kell,
hogy egyik eredménynél se nyerjen 2 szelvény. Próbáljunk meg így kitölteni 9
szelvényt! A próbálkozáshoz egy (3×3)×(3×3)-as táblázatban ábrázoljuk a lehetséges
eredményeket, illetve tippeket.
A táblázatban összesen 81 mező van, minden mező egy lehetséges eredménynek felel
meg. Az, hogy az adott mező melyik "sorhármasban" van, megmondja,
hogy mi az első mérkőzés végeredménye; a sorhármason belüli sor a második
mérkőzés végeredményére utal; az oszlophármas a harmadik, azon belül az
oszlopszám a negyedik meccs végeredményét jelzi.
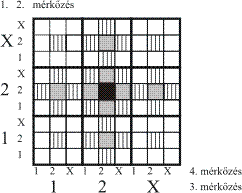
A kitöltött szelvénynek megfelelő mezőt befeketítjük. Ennél az eredménynél lenne a szelvény
telitalálatos. Szürkével jelöljük azokat az eredményeket, amelyek 3 találatosak
lennének. Ezeket nem szabad befeketíteni. Bevonalkázzuk azokat a mezőket,
amelyek a szürkéktől csak 1 mérkőzés végeredményében térnek el. Ezeket a
továbbiakban nem szabad befeketíteni, mivel minden eredménynél csak egy
szelvény nyerhet (lehet 3 vagy 4 találatos).
Röviden a szabályok: a fekete mezőtől csak egy adatban eltérő mezők szürkék, a pontosan
két adatban eltérők vonalazottak.
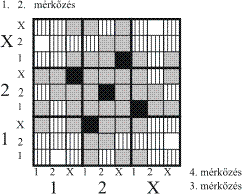
Mivel az 1-2-X eredmények egyenértékűek, és a mérkőzések egymástól függetlenek,
mindegy, hogy melyik az első kitöltött szelvény, ezért szimmetria-okokból válasszuk
elsőnek a középső mezőt (2222)! Ezután is tarthatjuk magunkat a szimmetriához,
még 4-4 szelvény kellene, esélyünk van 90°-os forgásszimmetriára. Ezért
bejelölünk a középponthoz legközelebb lévő még kitölthető szelvényt, rögtön a
forgásszimmetria szerint négyet (1X21, 21X1, X12X, 2X1X).
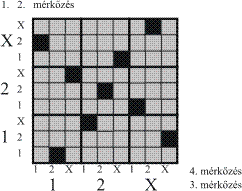
Lám, még szerencsénk is van: a négy mező együttes bejelölése sem okoz átfedést. Mint
látható, pont annyi lyuk van, amennyi szelvényt még el kell helyeznünk. Sikerült!
Megelégedéssel olvashatjuk le a megfelelő tippeket:
2222
1X21, 21X1, X12X, 2X1X
X211, 1112, 12XX, XXX2
E szelvényekkel biztos a legalább 3 találat, így 9 szelvény szükséges és
elégséges.
5.6 b) IV.
megoldása
Az előző megoldásban elején láttuk, hogy legalább 9 szelvény szükséges, és 9 szelvény
pontosan akkor oldja meg a feladatot, ha nincs olyan "eredmény",
amely a 9 szelvény közül kettőtől is csak egy mérkőzés eredményében tér el. Ez
épp azt jelenti, hogy a 9 szelvény 1-hiba javító kódot alkot. Ezek szerint a
4.6 feladatra adott megoldások bármelyike optimális szelvényeket szolgáltat,
csak a 0-kat kell X-re cserélni.
Megjegyzés
(Tökéletes kódok)
Tekintsünk k
különböző karaktert, és a belőlük alkotható összes n hosszú sorozatok,
"szavak", H halmazát. Úgy is tekinthetjük, mintha n
mérkőzésünk lenne és mindegyiknek k-féle eredménye lehetne. Legyen r
rögzített pozitív egész, és h a H eleme, azaz tetszőleges szó. "h középpontú r sugarú
körlapon" azoknak a szavaknak a halmazát értjük, amelyeknek h-tól
való Hamming távolsága legfeljebb r. A "kódelmélész" arra
törekszik, hogy minél több szót találjon úgy, hogy a köréjük írt r sugarú
körlapok diszjunktak legyenek. r = 1 esetén pld így 1-hiba javító kódot
kap. A "totózó" célja ezzel némileg ellentétes: ő szavaknak egy olyan
készletét keresi, amelyek köré írt r sugarú körlapok lefednek minden
szót, nem marad ki egy "eredmény" sem. Így ő olyan optimális
szelvény-készletet állít elő, amellyel biztosan nyer, ha r találatot
enged a telitalálatból. Bizonyos (k, n, r) számhármasoknál
céljukat ugyanannyi szóval, ugyanazzal a szókészlettel érik el. Az ilyen
szókészletek a tökéletes kódok.
5.7
A szenvedélyes játékosok már régóta
keresik az olyan nyerőesélyes tipprendszereket, úgynevezett totókulcsokat,
mint amilyet az 5.6 feladatban is kerestünk. Mégis, már "kicsinek"
tűnő esetekben sem ismeretes, hogy legkevesebb hány szelvény kell bizonyos
számú találat eléréséhez.
Az alábbi táblázat[1]
mutatja, hogy mit tudott a világ 1995-ben. n a mérkőzések számát jelöli,
r pedig azt mutatja, hogy legfeljebb hány találatot engedünk ki a
kezünkből. Az 5.6 feladat az n = 4, r =1 esetnek felel meg (k =
3).
| n/r |
1 |
2 |
3 |
| 1 |
1 |
|
|
| 2 |
3 |
1 |
|
| 3 |
5 |
3 |
1 |
| 4 |
9 |
3 |
3 |
| 5 |
27 |
8 |
3 |
| 6 |
63-73 |
12-17 |
6 |
| 7 |
150-186 |
26-34 |
7-12 |
| 8 |
393-486 |
52-81 |
13-27 |
| 9 |
1048-1356 |
128-219 |
25-54 |
| 10 |
2818-3645 |
323-558 |
57-108 |
| 11 |
7767-9477 |
729 |
115-729 |
| 12 |
21395-27702 |
1919-2187 |
282-729 |
| 13 |
59049 |
5062-6561 |
609-1215 |
Látható, hogy
elég kevés konkrét eredmény ismert. Az alábbi kérdés az egyik pontos eredményre
kérdez rá.
Feladat
Mutassuk meg, hogy a 13 mérkőzésből álló totón legalább 59049 szelvényt kell kitölteni ahhoz,
hogy biztosan elérjünk legalább 12 találatot!
Megoldás
Összesen 313-féle szelvény lehetséges. Egy szelvénnyel 1 + 2·13 = 27 = 33 esetben van
legalább 12 találatunk, így legalább 313/33 = 310
= 59049 szelvényre van szükség.
2. házi feladat
Kíséreljünk meg konstruálni 59049 megfelelő szelvényt.
Megjegyzés:
Látható, hogy k = 3 esetén akkor van lehetőség 1-hiba javító tökéletes kódra (r
= 1), ha 1 + 2n = 3s. Ha tehát s tetszőleges
pozitív egész,
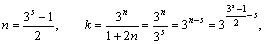
akkor az
egyszerű leszámlálás nem zárja ki tökéletes kód létezését.
3. házi feladat: 5.9
Most is az 1, 2, 3, ...16 számok közül
kell kitalálni egyet barkochba kérdésekkel. Kérdéseinket előre le kell írni és
nincs befolyásunk arra, hogy a gondoló milyen sorrendben nézi és válaszolja meg
azokat.[2]
Hány kérdéssel tudjuk biztosan kitalálni a gondolt számot, ha várhatóan egyszer
(legfeljebb egyszer) téves választ kapunk?
4. házi feladat: Hétszögminták
Ebben a feladatban egy
szabályos hétszög csúcsaira írunk 0-t vagy 1-et. Összesen 27=128
ilyen kitöltés van. A kitöltések egy I7 részhalmaza "7-szögre
ideális", ha
1. Ha h eleme I7 -nek, akkor h bármely (n·360°/7-kal
való) elforgatottja is I7-ben van.
2. Bármely két I7-beli kitöltés csúcsonként és mod 2 számított összege
is I7-ben van.
A kitöltéseknek hány "7-szögre ideális" részhalmaza van?
[1]
Forrás: H. Hämäläinen, I. Honkala, S. Lytsin, P. Östergøard, Football
Pools - A Game for Mathematicians, American Math. Monthly, August-Sept 1995,
579-588.
[2]
Ezzel az "Előző válaszod igaz volt?" - típusú kérdéseket akarjuk
kiszűrni. Tehát kérdés nem vonatkozhat a válaszok igazságtartalmára.




