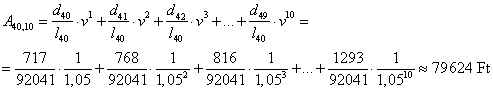Szászné Simon Judit:Aktuáriusi számítások
Pénzügyi és biztosítási matematika
Az aktuárius biztosítási matematikust jelent. Ilyen
végzettségű emberek bankoknál, biztosítóknál, nyugdíjpénztáraknál,
könyvvizsgálóknál és egyéb pénzzel kapcsolatos helyeken dolgoznak.
Ez az anyag a 2002-ben a győri Rátz László
Vándorgyűlésen elhangzott előadásom alapján készült, lényegében a diasorozatot
láthatjuk néhány kiegészítő kommentárral. Az alábbi felsorolás tartalmaz néhány
olyan címszót is, ami nem tárgya ennek az anyagnak, inkább csak a továbbhaladás
egy lehetséges irányát jelöli ki.
| Pénzügyi matematika |
Életbiztosítások matematikája |
- Kamat, diszkont
- Hiteltörlesztési tervek, teljes hiteldíj-mutató
- Járadékszámítás
- Pénzáramlások jelenértéke
- Évjáradékok jelenértéke
- Értékpapírok elméleti árfolyama
- Hozam és megtérülés
|
- Demográfiai alapfogalmak
- Halálozási görbék, várható élettartam
- Életbiztosítások alaptípusai és nettó egyszeri díjuk
- Évi díjfizetés mellett szükséges díjak
- Nyugdíj
- Bruttó díjak
- Díjtartalék, annak hozama és következményei
|
Ebben
az egyszerű bevezető tanulmányban kéttípusú, elemi számítási feladatokat fogunk
megoldani. Az első részben pénzügyi matematikából nézünk néhány hitelre,
kamatra vonatkozó példát, azután a biztosítási matematikából az
életbiztosítások alaptípusainak áttekintése után ezek nettó díját számoljuk ki.
Először
lássunk néhány feladatot pénzügyi matematikából. Ez olyan téma, amely régebben
a diákoknak is, ezért nekem is a nemszeretem témák közé tartozott. A
körülöttünk lévő világ változásával azonban az utolsó 8-10 évben megnőtt az
érdeklődés minden a pénzzel kapcsolatos ismeret, számítás iránt. Ez nem is
csoda, hiszen a bankok például a hitelek nyújtása esetén fantasztikus
kamatcsökkentéssel, betétlekötés esetén pedig fantasztikus kamatemeléssel
kápráztatnak el mindenkit. Közben általában nem vesszük észre az alsó sorban megbúvó
betűket: THM vagy EBKM, melyek az összehasonlíthatóságot szolgálják. A THM
jelentése teljes hiteldíj mutató, amely nagyjából azt mutatja meg, mennyibe
kerül valójában a hitel. Ez a szám a hitel kamatánál általában jóval nagyobb
szám, hiszen a hitelen kívül megfizetjük az elbírálási költséget, a kezelési
költséget, az éves zárási költségeket és ki tudja még mit.
Az EBKM jelentése egységesített betéti kamatlábmutató. Az
EBKM és a pénzintézet által meghirdetett betéti kamatláb annyiban tér el
egymástól, hogy míg az éves banki kamatlábak általában 360 napra vetítve
kerülnek megállapításra, s egy évnél rövidebb futamidő esetén a kamat
visszaforgatását, tőkésítését nem veszik figyelembe, addig az EBKM egy adott
év, azaz 365 nap elteltével mutatja az elhelyezett betét után fizetendő
kamatösszeg nagyságát. Elképzelhető azonban az is, hogy a bank nem éves, hanem
rövidebb vagy hosszabb időszak kamatlábát közlik. Betétlekötés esetén érdemes
tehát a bankok kínálatában ezt a mutatót keresni
Most lássunk néhány példát!
1.példa
50000 forintot szeretnénk 7 évre befektetni. Három befektetés közül választhatunk:
a) minden év végén hozzátesznek a pénzünkhöz egy fix
összeget, 7500 forintot, ami az eredeti összeg 15%-a
b) 11%-os kamatos kamatot fizetnek
c) az első évben 17% kamatot kapunk, majd évente 2%-kal
csökken, míg eléri a 7 %-ot, és ennyit kamatozik az utolsó évben is.
Melyik befektetés a legkedvezőbb?
Megoldás
Az első esetben 52500 Ft a kamat, azaz 102 500 forintunk
lett.
A másodiknál az összeg az eredeti 1,117 ~ 2,076-szorosa lesz, ami
103 808 Ft.
A harmadik esetben a betett összeg 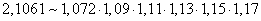 – szorosa, azaz 105 505 Ft, tehát ez a
legjobb.
– szorosa, azaz 105 505 Ft, tehát ez a
legjobb.
Ha az utolsó évben is 2%-kal csökkenne a kamat, akkor már a második eset a
legjobb, de ha csak 6%-ra csökken, hajszállal a harmadik befektetés nyer.
2.példa
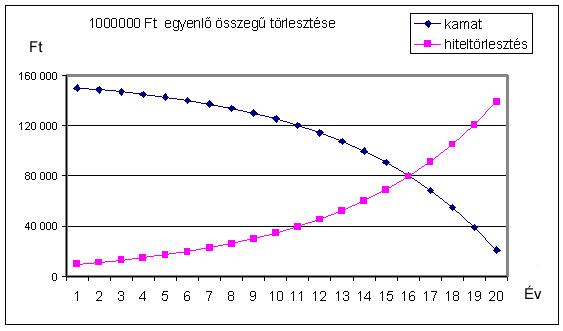
Egymillió forint összegű
jelzálogkölcsönt veszünk fel 20 évre 15 %-os kamatra. Mennyi az évi törlesztő
rész? Mennyi fordítódik a kamatfizetésre, és mennyi az adósság törlesztésére?
Ábrázolja grafikonon!
Megoldás
Az évente fizetendő részlet (x) kiszámítása: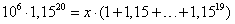 ahonnan
x = 159761,5 Ft.
ahonnan
x = 159761,5 Ft.
Jelenérték-számítás
Kölcsöntörlesztés
3. példa
Melyik a legelőnyösebb?
A : a pénzt évi 21%-os kamatra tesszük be, és évenként tőkésítenek
B : a pénzt évi 20%-os kamatra tesszük be, és félévenként tőkésítenek
C : a pénzt évi 19,5%-os kamatra tesszük be, és havonta tőkésítenek
D : a pénzt évi 20%-os kamatra tesszük be, és naponta tőkésítenek.
Megoldás
A: 1,21
B: (1+0,2/2)2=1,21
C: (1+0,195/12)12 =1,2134
D: (1+0,2/365)365=1,2213
Látható, hogy előnyösebb, ha
19,5%-os kamat mellett havonta tőkésítenek, az évente egyszer tőkésített 21%-os
kamatnál.
Felmerülhet a kérdés, hogy ha
mondjuk percenként tőkésítenének 20%-os kamat mellett, akkor elérjük-e a 23%-ot.
A válasz sajnos az, hogy nem, mivel 20%-os kamat mellett n tőkésítés
esetén a nominális
kamat (1+0,2/n)n , ami tart 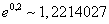 -hez.
-hez.
Biztosítás
Nem a legnépszerűbb téma. Akkor
találkozunk a biztosítókkal, ha meghalt, leégett, ellopták, balesetet
szenvedett. Mégis úgy gondolom az egyik legjobb lehetőség a statisztika
hasznának bemutatására, a mostani elvárásnak megfelelő “életszerű” példák
konstruálására.
A biztosítási üzletet
többféleképpen szokták felosztani. Mi most egy lehetséges felosztást vázolunk
néhány fontos és alapvető eltérést említve.
| ÁG |
ÉLET |
NEM-ÉLET |
| Tartam |
5-25 év |
1 év |
| Káringadozás |
kicsi |
nagy |
| Felmondás |
nincs |
évfordulón |
| |
összegbiztosítás |
kárbiztosítás |
A legalsó sor azt jelenti, hogy
míg például egy autónál a biztosító a ténylegesen bekövetkezett kárértéket
(vagy annak meghatározott részét) fizeti ki, az életbiztosításokat előre
meghatározott összegre kötik, értelmetlen arról beszélni, kinek mennyit ér az
élete.
A továbbiakban csak az egyszerűbben kalkulálható
életbiztosításokkal foglalkozunk.
Demográfiai alapfogalmak
Halálozási
valószínűség (
qx,1): annak valószínűsége, hogy egy
x
éves egyén meghal az
x+1-edik születésnapja előtt
Megélési
valószínűség (px,1): annak valószínűsége, hogy egy x
éves egyén megéli az x+1-edik születésnapját
Halandósági táblázat tartalmazza, hogy egy 100 000 fős
populációt alapul véve hányan érnék meg az adott x éves kort. Ezt a
számot lx jelöli.
Azoknak az x
éves egyének számát, akik meghaltak az x+1-edik születésnapjuk előtt dx
jelöli.
(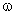 jelöli
a halandósági táblázat készítésénél figyelembe vett legmagasabb életkort, és
jelöli
a halandósági táblázat készítésénél figyelembe vett legmagasabb életkort, és  )
)
Példaként az 1993-as férfi és női halandósági táblázat
két-két oszlopát mutatjuk itt be.
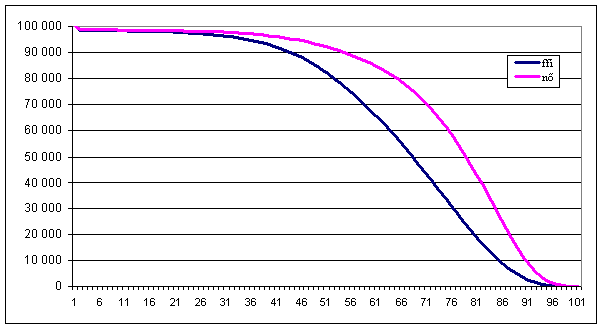
Halandósági tábla ( 1993 )
|
|
|
|
|
|
|
Férfi |
Nő |
| Belépési életkor (x) |
lf(x) |
df(x) |
ln(x) |
dn(x) |
| 0 | 100 000 | 1 366 | 100 000 | 1 106 |
| 1 | 98 634 | 81 | 98 894 | 67 |
| 2 | 98 553 | 56 | 98 827 | 45 |
| 3 | 98 497 | 49 | 98 782 | 44 |
| 4 | 98 448 | 30 | 98 738 | 29 |
| 5 | 98 418 | 22 | 98 709 | 16 |
| 6 | 98 396 | 24 | 98 693 | 13 |
| 7 | 98 372 | 28 | 98 680 | 15 |
| 8 | 98 344 | 31 | 98 665 | 18 |
| 9 | 98 313 | 31 | 98 647 | 19 |
| 10 | 98 282 | 29 | 98 628 | 18 |
| 11 | 98 253 | 24 | 98 610 | 16 |
| 12 | 98 229 | 20 | 98 594 | 16 |
| 13 | 98 209 | 22 | 98 578 | 22 |
| 14 | 98 187 | 37 | 98 556 | 37 |
| 15 | 98 150 | 43 | 98 519 | 33 |
| 16 | 98 107 | 53 | 98 486 | 33 |
| 17 | 98 054 | 66 | 98 453 | 34 |
| 18 | 97 988 | 79 | 98 419 | 35 |
| 19 | 97 909 | 93 | 98 384 | 35 |
| 20 | 97 816 | 105 | 98 349 | 37 |
| 21 | 97 711 | 114 | 98 312 | 38 |
| 22 | 97 597 | 121 | 98 274 | 39 |
| 23 | 97 476 | 129 | 98 235 | 41 |
| 24 | 97 347 | 137 | 98 194 | 44 |
| 25 | 97 210 | 149 | 98 150 | 49 |
| 26 | 97 061 | 163 | 98 101 | 56 |
| 27 | 96 898 | 177 | 98 045 | 64 |
| 28 | 96 721 | 194 | 97 981 | 73 |
| 29 | 96 527 | 215 | 97 908 | 84 |
| 30 | 96 312 | 241 | 97 824 | 97 |
| 31 | 96 071 | 272 | 97 727 | 111 |
| 32 | 95 799 | 307 | 97 616 | 127 |
| 33 | 95 492 | 345 | 97 489 | 144 |
| 34 | 95 147 | 386 | 97 345 | 163 |
| 35 | 94 761 | 433 | 97 182 | 181 |
| 36 | 94 328 | 485 | 97 001 | 200 |
| 37 | 93 843 | 541 | 96 801 | 219 |
| 38 | 93 302 | 601 | 96 582 | 240 |
| 39 | 92 701 | 660 | 96 342 | 259 |
| 40 | 92 041 | 717 | 96 083 | 281 |
| 41 | 91 324 | 768 | 95 802 | 300 |
| 42 | 90 556 | 816 | 95 502 | 319 |
| 43 | 89 740 | 863 | 95 183 | 339 |
| 44 | 88 877 | 916 | 94 844 | 361 |
| 45 | 87 961 | 978 | 94 483 | 387 |
| 46 | 86 983 | 1 051 | 94 096 | 420 |
| 47 | 85 932 | 1 130 | 93 676 | 454 |
| 48 | 84 802 | 1 212 | 93 222 | 492 |
| 49 | 83 590 | 1 293 | 92 730 | 530 |
| 50 | 82 297 | 1 369 | 92 200 | 568 |
| 51 | 80 928 | 1 437 | 91 632 | 601 |
| 52 | 79 491 | 1 500 | 91 031 | 632 |
| 53 | 77 991 | 1 561 | 90 399 | 664 |
| 54 | 76 430 | 1 623 | 89 735 | 702 |
| 55 | 74 807 | 1 692 | 89 033 | 749 |
| 56 | 73 115 | 1 764 | 88 284 | 804 |
| 57 | 71 351 | 1 836 | 87 480 | 867 |
| 58 | 69 515 | 1 908 | 86 613 | 934 |
| 59 | 67 607 | 1 980 | 85 679 | 1 005 |
| 60 | 65 627 | 2 048 | 84 674 | 1 079 |
| 61 | 63 579 | 2 113 | 83 595 | 1 150 |
| 62 | 61 466 | 2 172 | 82 445 | 1 219 |
| 63 | 59 294 | 2 228 | 81 226 | 1 293 |
| 64 | 57 066 | 2 281 | 79 933 | 1 378 |
| 65 | 54 785 | 2 333 | 78 555 | 1 479 |
| 66 | 52 452 | 2 382 | 77 076 | 1 593 |
| 67 | 50 070 | 2 425 | 75 483 | 1 714 |
| 68 | 47 645 | 2 460 | 73 769 | 1 842 |
| 69 | 45 185 | 2 486 | 71 927 | 1 977 |
| 70 | 42 699 | 2 502 | 69 950 | 2 118 |
| 71 | 40 197 | 2497 | 67832 | 2247 |
| 72 | 37 700 | 2 471 | 65 585 | 2 362 |
| 73 | 35 229 | 2 442 | 63 223 | 2 483 |
| 74 | 32 787 | 2 420 | 60 740 | 2 626 |
| 75 | 30 367 | 2 411 | 58 114 | 2 802 |
| 76 | 27 956 | 2 500 | 55 312 | 3 069 |
| 77 | 25 456 | 2 431 | 52 243 | 3 208 |
| 78 | 23 025 | 2 356 | 49 035 | 3 340 |
| 79 | 20 669 | 2 275 | 45 695 | 3 460 |
| 80 | 18 394 | 2 184 | 42 235 | 3 560 |
| 81 | 16 210 | 2 083 | 38 675 | 3 634 |
| 82 | 14 127 | 1 971 | 35 041 | 3 675 |
| 83 | 12 156 | 1 846 | 31 366 | 3 675 |
| 84 | 10 310 | 1 708 | 27 691 | 3 626 |
| 85 | 8 602 | 1 557 | 24 065 | 3 523 |
| 86 | 7 045 | 1 396 | 20 542 | 3 362 |
| 87 | 5 649 | 1 227 | 17 180 | 3 142 |
| 88 | 4 422 | 1 054 | 14 038 | 2 868 |
| 89 | 3 368 | 882 | 11 170 | 2 547 |
| 90 | 2 486 | 715 | 8 623 | 2 192 |
| 91 | 1 771 | 559 | 6 431 | 1 820 |
| 92 | 1 212 | 420 | 4 611 | 1 450 |
| 93 | 792 | 300 | 3 161 | 1 102 |
| 94 | 492 | 204 | 2 059 | 793 |
| 95 | 288 | 130 | 1 266 | 538 |
| 96 | 158 | 78 | 728 | 340 |
| 97 | 80 | 43 | 388 | 198 |
| 98 | 37 | 21 | 190 | 106 |
| 99 | 16 | 10 | 84 | 51 |
| 100 | 6 | 6 | 33 | 33 |
Tanulságos az adatokat grafikonon
is megnézni.
Halandósági görbe
Életbiztosításban használt alapfogalmak
Technikai kamat (
i): az a kamat, amellyel a biztosító számol, hogy azt minimálisan el fogja
érni.
Várható élettartam (
ex): az
x éves egyének még
várhatóan ennyi évet élnek.
Legfontosabb közülük az
x = 0 eset, amit születéskor várható élettartamnak
hívnak.
Ezt nemzetközi
összehasonlításban is fontos vizsgálni (az EU ötödik összehasonlító adata), de
sokatmondó lehet egy országra nézve az idősora is.
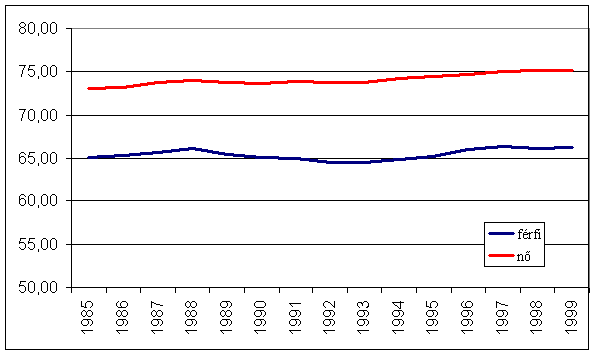
Születéskor
várható átlagos élettartam alakulása Magyarországon
| Év | férfiak | nők |
| 1985 | 65,09 | 73,07 |
| 1986 | 65,3 | 73,21 |
| 1987 | 65,67 | 73,74 |
| 1988 | 66,16 | 74,03 |
| 1989 | 65,44 | 73,79 |
| 1990 | 65,13 | 73,71 |
| 1991 | 65,02 | 73,83 |
| 1992 | 64,55 | 73,73 |
| 1993 | 64,53 | 73,81 |
| 1994 | 64,84 | 74,23 |
| 1995 | 65,25 | 74,5 |
| 1996 | 66,06 | 74,7 |
| 1997 | 66,35 | 75,08 |
| 1998 | 66,14 | 75,18 |
| 1999 | 66,32 | 75,13 |
Grafikusan ez a következőt jelenti:
Nemzetközi összehasonlításban sem állunk e téren túl jól.
SZÜLETÉSKOR VÁRHATÓ ÉLETTARTAMOK EGYES ORSZÁGOKBAN
| Ország | Férfiak | Nők |
| India | 62,5 | 71,5 |
| Törökország | 65 | 69,6 |
| Románia | 66,1 | 73,7 |
| MAGYARORSZÁG | 66,3 | 75,1 |
| Bulgária | 67,1 | 74,9 |
| Kína | 68,6 | 71,5 |
| Lengyelország | 68,8 | 77,5 |
| Szlovákia | 69 | 77 |
| Csehország | 71,4 | 78,1 |
| Dánia | 73,8 | 79,3 |
| Finnország | 73,8 | 81 |
| Ausztria | 74,3 | 80,8 |
| Nagy-Britannia | 74,7 | 80,2 |
| Franciaország | 74,8 | 82,7 |
| Hollandia | 75,3 | 81,2 |
| Görögország | 75,9 | 81,2 |
| Japán | 77 | 83,4 |
| Ausztrália | 77,2 | 83,2 |
| Svájc | 79 | 82,1 |
Ez egy 40 országot tartalmazó lista részlete, ahol
Magyarország a férfiak között a 6. legrosszabb eredményt, a nők közt a 9.-et
érte el. A teljes lista három legjobbja valóban Svájc, Japán és Ausztrália.
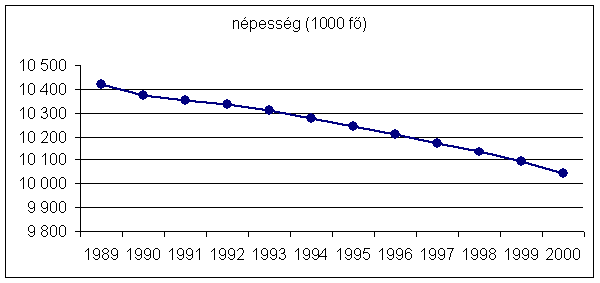
Azt gondolom, az
alacsony várható élettartam és a szülések csökkenő számát tekintve nem is lehet
váratlan a népesség számának alakulása.
Most térjünk rá az életbiztosítási alapbiztosítások
áttekintésére.
Életbiztosítások alaptípusai
Kockázati életbiztosításnak hívjuk azt a biztosítást,
amelyben a szerződésben megjelölt személy megkapja a biztosítási összeget
(amelyre a szerződés szólt), ha a biztosítási tartam alatt a biztosított
meghal, de kifizetés nélkül szűnik meg, ha a biztosított megéri a tartam végét.
Elérési életbiztosítás olyan biztosítás, amelynél a
biztosított (vagy akit megjelöl) megkapja a biztosítási tartam végén a
biztosítási összeget, amelyre a szerződés szólt, ha él, de kifizetés nélkül
szűnik meg, ha a tartam alatt a biztosított meghal.
A vegyes
életbiztosítás ugyan nem alaptípus, hiszen egy kockázati és egy elérési
biztosítás együttese, de ez az egyik leggyakoribb biztosítástípus. Tehát ha a
biztosított a tartam alatt meghal, akkor a haláleset után (most a számítás
egyszerűsítése céljából az év végén), ha nem, akkor a tartam végén fizeti ki a
biztosítási összeget.
Járadékbiztosítás olyan biztosítás, amely a
megkötésekor befizetett összeg függvényében meghatározott ideig (akár
élethosszig) éves (vagy havi) előre meghatározott összegű kifizetést teljesít,
ha a biztosított még él. (Felfogható tehát elérési biztosítások sorozataként.)
Díjkalkuláció alapelve
A díjszámítás alapja az
ekvivalencia elv, ami azt
mondja ki, hogy
A bevételek
várható értékének jelenértéke = a kiadások várható értékének jelenértékével.
A díjkalkulációt általában érdemes 1 egységnyi összegre
végezni, hiszen S egységnyi összegre az 1 egységnyire fizetendő díj S-szerese
jön ki.
Egyszeri díjas életbiztosítások
Jelölések, alapösszefüggések:
A: a biztosítás egyszeri díja
n: a biztosítás tartama
v: diszkonttényező (=1/(1+i) , ahol i a
technikai kamat)
Megélési és halálozási
valószínűségek:
px,1 = lx+1
/ lx és qx,1 = dx / lx
= ( lx – lx+1 ) / lx
px,n = lx+n
/ lx és qx,n = ( lx – lx+n
) / lx
4. példa
Mekkora a valószínűsége annak, hogy egy 40 éves
férfi 3 éven belül meghal?
Megoldás
1-89740/92041=
0,0250 =2,5%
5. példa
Mekkora a valószínűsége annak, hogy egy 40 éves
férfi még 8 évig él, de azután két éven belül meghal?
Megoldás
(82297-79491)/87961=2806/87961=0,0319
≈ 3,2 %
Egyszerűsítő feltevések:
- Egyszeri díjas biztosítás ⇒
teljes díj a tartam elején a biztosítóhoz befolyik
- Mindenki január 1-jén született
- Minden kifizetés az év végén történik (= mindenki december 31-én halt meg)
A kockázati életbiztosítás egyszeri díja
Ha az x éves egyén n
évre köt biztosítást, akkor az ekvivalencia-egyenlet szerint a díj:
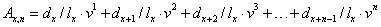
6. példa
Egy 40 éves férfi 1 000 000 Ft-ot szeretne
kapni, ha 10 éven belül meghal. Mennyi a biztosítás nettó egyszeri díja, ha a
technikai kamat 5%?
Megoldás
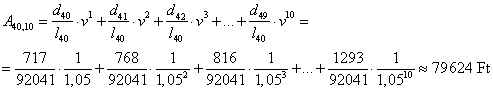
Whole life biztosítás: a
biztosítási összeget az ügyfél halálakor kell kifizetni (azaz élethosszig szóló
biztosítás).
Az elérési életbiztosítás díja
Ha az x éves egyén n
évre köt biztosítást, akkor az elérési biztosítás ekvivalencia-egyenlete:
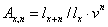
7. példa
Egy 40 éves férfi 10 év múlva 100 000 Ft-ot
szeretne kapni, ha még él. Mennyi a biztosítás nettó egyszeri díja, ha a
technikai kamat 5%?
Megoldás
Ez egy elérési biztosítás, ennek díja =100 000Ft diszkontált
értéke szorozva a megélés valószínűségével, azaz
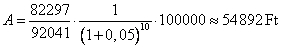
A vegyes
életbiztosítás díja = az elérési díj + a kockázati díj
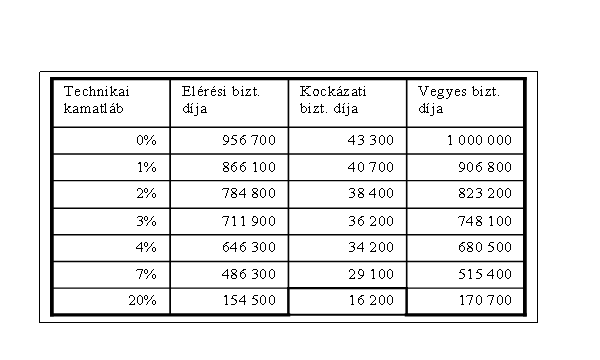
A technikai kamat jelentőségére
az alábbi táblázattal kívánok rámutatni.
A technikai kamat és a díj összefüggése
(30 éves belépési kor, 10 éves tartam, 1000 000 Ft biztosítási összeg)
Látható, milyen erős díjcsökkentő tényező, ezért a
teljesíthetetlen ígéretek megelőzése érdekében maximális mértékét a
pénzügyminiszter határozza meg, ill. módosítja.
Egyszeri díjas, azonnal induló életjáradék díja
Jelölje ax az azonnal induló, éves
kifizetésű, az év elején fizető életjáradék-biztosítás egyszeri díját, amely
évi 1 Ft járadékot fizet a biztosított haláláig.
(a biztosított belépési kora x )
Ekkor az ekvivalencia-egyenlet:
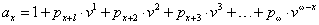
Például ha egy 60 éves férfi évi 10 000 Ft-ot szeretne kapni
haláláig, akkor 3,5%-os technikai kamat mellett, ennek a nettó díja 113 380 Ft.
Ha azonban egy férfi 30 éves korában köti azt a járadékbiztosítást, amely csak
60 éves korától fizeti a 10 000 Ft-ot az előző feltétellel, akkor csak 31
345 Ft-ot kell befizetnie.
A
biztosítás díja rendszeres díjfizetés esetén
- Az évenkénti díjfizetés felfogható úgy, mintha az ügyfelek
járadékot fizetnének a biztosítónak a díjfizetés tartama alatt.
- Ezért a rendszeres díjfizetés mellett fizetendő díjat egy
tetszőleges biztosításnál úgy kapjuk az egyszeri díjból, hogy elosztjuk a
járadéktényezővel, amelyet abból számolhatunk ki, hogy az egyszeri díjat hány
évi díjfizetés mellett fizetjük majd ki.
A nyugdíjról

Ha az eddigieket végiggondoljuk, a nyugdíj nem más, mint egy
elérési biztosítás a nyugdíjkorhatárig, onnan pedig egy azonnal induló,
élethosszig tartó járadékbiztosítás.
A nyugdíjrendszerek közötti egyik alapvető különbség, hogy
milyen módszerrel valósítják meg, hogyan érik el, hogy a nyugdíj folyósításához
szükséges pénzeszköz rendelkezésre álljon.
A nyugdíjrendszerek egy lehetséges csoportosítása a
következő:
Felosztó-kirovó rendszer
Az az évi befizetések teremtik meg az az évi kifizetések
fedezetét. A befizetések nagyságát úgy állapítják meg, hogy az éppen fedezze a
tárgyévi kifizetéseket. Meg kell jegyezni, hogy a valóságban ez meglehetősen
nehéz, hiszen csak év végére lesz pontosan ismert a tárgyévi kifizetések
nagysága, ráadásul a járulékkulcsot sem lehet évente módosítani. Így aztán az
ilyen rendszerekben képződhet valamennyi tőke, kellemetlenebb esetekben hiány
az adott év folyamán. A magyarországi társadalombiztosítási rendszer ilyen
elven működik, és évek óta hiány képződik a rendszerben.
Terminális tőkefedezeti rendszer
A befizetés akkor történik, amikor a kifizetés elkezdődik,
így a befizetés pontosan olyan mértékű, hogy egy összegben megteremti a teljes
kifizetés várható fedezetét. (Pl. valaki évjáradékot vásárol egy biztosító
intézettől.)
Iniciális tőkefedezeti rendszer
A rendszerbe történő belépéskor egyösszegű befizetés teremti
meg a későbben (pl. nyugdíjba vonuláskor) kezdődő kifizetések várható
fedezetét.
Rendszeres hozzájáruláson alapuló tőkefedezeti rendszer
A belépéstől a nyugdíjba vonulásig rendszeresen befizetett
hozzájárulás teremti meg az összes későbbi várható kiadás fedezetét. (
Magán-nyugdíjpénztár)
Ez ennek a témának néhány bevezető gondolata.
Kérdéseivel, megjegyzéseivel bátran keressen meg a következő
e-mail címen: <simonj@fazekas.hu>
![]() – szorosa, azaz 105 505 Ft, tehát ez a
legjobb.
– szorosa, azaz 105 505 Ft, tehát ez a
legjobb.