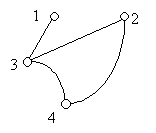
Ha meg akarjuk keresni azt, ami az elmondott feladatokban közös, érdemes a következőt tennünk: Ábrázoljuk az embereket, a városokat, illetve a telefonállomásokat egy-egy ponttal. Két embert ábrázoló pontot „összekötünk egy éllel” (azaz például egy egyenes szakasszal), ha játszottak egymással (az 1. feladat megfogalmazásában), ha ismerik egymást (az 1a) feladat megfogalmazásában), ha nem ismerik egymást (3a) feladat), illetve ha kezet fogtak egymással (3b )feladat), két várost jelző pontot összekötünk egy éllel, ha van közöttük közvetlen repülőjárat (a 3c) feladat esetében), illetve két telefonállomást jelző pontot összekötünk egy éllel, ha volt közöttük telefonkapcsolat az adott napon. Egyáltalán nem érdekes, hogy milyen alakja van az „élnek”, amellyel a pontokat összekötjük: lehet az él egy egyenes szakasz, de lehet egy görbe is, ennek semmilyen szerepe nincs, csak az számít, hogy „fut-e él” a két pont között vagy sem.