41.          Ha a háromszögek súlypontjait vesszük egy gráf pontjainak és két ilyen pontot összekötünk, ha a megfelelő háromszögek határosak, akkor az így kapott gráf fa.

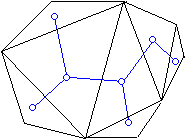
Ugyanis a behúzott átlók és a gráf élei között egy-egyértelmű megfeleltetés van, másrészt a gráf nyilván összefüggő, n–2 pontja van (mert ennyi háromszög van) és eggyel kevesebb éle, mert n–3 átlót húztunk be. Tehát ez a gráf fa, amelynek n>3 miatt van éle, így a 39a. feladat szerint legalább két elsőfokú pontja van. Az elsőfokú pontnak pedig olyan háromszög felel meg, amelyet csak egy átló határol, ez pedig pontosan akkor fordul elő, ha a háromszög határa két oldal és egy legrövidebb átló. Ha n > 4, akkor a két elsőfokú pont nem szomszédos, így a két legrövidebb átló nem lehet azonos. (Ha n=4, akkor a két háromszögnek ugyanaz az átló a határa.)