47.          A feladat gráfelméleti nyelven így hangzik: egy gráfban minden pont foka legfeljebb öt és bármely két pont távolsága legfeljebb négy(!). Hány pontja lehet maximálisan a gráfnak?

Gondoljuk meg először, hogy miért biztos egyáltalán, hogy nem lehet akármilyen sok pontja. A megoldásra nyilvánvalóan kínálkozik a szélességi faváz. Keressük meg egy tetszőleges x ponthoz tartozó szélességi favázát a gráfnak. Miután minden pont foka legfeljebb öt, ezért az első szinten legfeljebb öt pont lesz és minden további szinten az előző szint pontszámának legfeljebb négyszerese. Másrészt bármely két pont távolsága legfeljebb négy, ezért maximálisan négy szint lesz az x gyökéren kívül. Tehát valóban csak korlátos sok pontja lehet a gráfnak. Egyelőre az 1+5+20+100+400=526 felső korlátot kaptuk, ez azonban még túl sok pont: ha lerajzoljuk a fát, kiderül, hogy ebben a legfelső szint pontjai között olyanok is vannak, amelyek egymástól négy helyett nyolc távolságra vannak. Tehát ennél csak jóval kevesebb pont lehet. Megpróbálhatjuk ezt az eljárást folytatni, de akkor meg kell gondolnunk, hogy mit csinálunk az esetleg fellépő körökkel. Célszerűbb megpróbálni ügyesen megválasztani az x pontot: úgy, hogy biztosan alacsonyabb legyen a szélességi faváz. S valóban: vegyük a gráf (egyik) leghosszabb útját. Ez a feladat feltétele szerint legfeljebb négy hosszúságú. Feltehetjük, hogy potosan négy hosszúságú (MIÉRT?!). Legyen x ennek középső pontja. Azt állítjuk, hogy az x gyökerű szélességi faváz már csak kétszintes lehet. Tegyük fel ugyanis, hogy van egy y pont a faváz harmadik szintjén. Az y pontból a gyökérhez vezető út az első szintről pontosan egy pontot tartalmaz, legyen ez z. Az a leghosszabb út, amelynek x a középső pontja, két kettő hosszú, x-ből induló útra bomlik, s ezek közül (legalább) az egyik nem tartalmazza z-t, s így az yz út egyetlen pontját sem. Ha ezt az utat hozzáillesztjük az y-ből x-be menő úthoz, akkor egy öt hosszú utat kapunk, ami ellentmond a feladat feltételének.

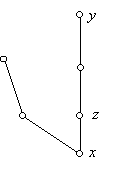
Tehát az x gyökerű szélességi faváz valóban legfeljebb kétemeletes. Ezért legfeljebb 1+5+20=26 pontja van.

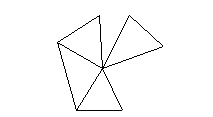
Ha felrajzoljuk azt a fát, amelynek első szintén öt pont van és minden pontjából négy második szintű ponthoz indul él, akkor ez a gráf megfelel a feladat feltételeinek. Tehát 26 a pontos válasz.