48.          a) Nyilván elég az állítást a gráf feszítő fájára igazolni (MIÉRT?). Vegyük a gráf (egyik) leghosszabb, 2k hosszú útját és egészítsük ki ezt favázzá. Ezt a 34. feladat szerint megtehetjük. Nyilván a faváznak is ez a(z egyik) leghosszabb útja. Vegyük a középső pontját, legyen ez x, két útbeli szomszédja y és z. Ha x-ből indulna ki k-nál hosszabb U út a favázban (vagyis a faváz magassága nagyobb volna k-nál), akkor ez az út y és z közül csak az egyiket tartalmazhatja, például y-t, és minden további pontja y utódja volna. De akkor ezt az U utat hozzáillesztve a leghosszabb út z-t tartalmazó „félútjához” kapnánk egy 2k-nál hosszabb utat, ami ellentmondás. Ezzel bebizonyítottuk az állítást.

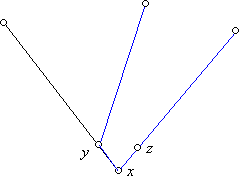
Kérdés: hol használtuk ki, hogy favázat vettünk az elején?

b) Ez nyilvánvalóan nem igaz, már akkor sem, ha a gráf egy út: például a végpontjai között ugyanakkora a távolság, mint a leghosszabb út hossza.