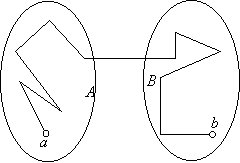
Legyen először a gráf összefüggő és bontsuk a gráf csúcsainak halmazát két nem üres részre: legyen a két rész A és B. Legyen a és b a két részhalmaz egy-egy csúcsa. Az összefüggőség miatt vezet közöttük út. Az út kezdőpontja és végpontja különböző részhalmazokban van, tehát van olyan él is, amelynek egyik végpontja az egyik halmazban van, másik végpontja a másikban. Ezt akartuk bizonyítani.

(D’) BIZONYÍTÁSA:

Ha van két nem üres ponthalmaz, A és B, amelyek között nem fut él, akkor a gráf nem lehet összefüggő, mert A semelyik pontjából nem vezet út B egyik pontjába sem. Ha viszont a gráf nem összefüggő, akkor van két pontja, amely között nem vezet út. Legyen ez a két pont a és b. Ekkor az a-ból úttal elérhető pontok halmaza és a komplementere sem üres (az elobbibe mindenképp beletartozik a, az utóbbiba b). E két halmaz között pedig nem vezet él.