AZ (E) ÁLLÍTÁS BIZONYÍTÁSÁHOZ eloször egy eljárást definiálunk, amely a G fa, és általánosabban egy összefüggő G gráf egy G’ részgráfját választja ki:
1. LÉPÉS:
Válasszuk ki a G gráf egy tetszőleges x1 pontját, ez a pont pontja lesz a G’ részgráfnak.
2. LÉPÉS:
Ha a gráfnak x1-en kívül nincs több pontja, befejezzük az eljárást.
Ha a gráfnak x1-en kívül is van pontja, akkor keressünk egy olyan x2 pontot, amely össze van kötve x1-gyel. Ilyen pontnak kell lennie, különben a gráf nem volna összefüggő. Az x2 pontot és az x1x2 élt beválasztjuk a G’ részgráfba.
k. LÉPÉS:
Tegyük fel, hogy az x1, x2, …, xk–1 pontokat már kiválasztottuk.
Ha az {x1, x2, …, xk–1}=A halmaz tartalmazza a G gráf összes pontját, akkor befejezzük az eljárást.
Ha az {x1, x2, …, xk–1}=A halmaz nem tartalmazza a G gráf összes pontját, akkor (D) szerint van olyan él, amely A és a gráf többi pontja között fut, vagyis egy A-beli xi pontot köt össze egy A-n kívüli xk ponttal. Az xk pontot és az xixk élt beválasztjuk a G’ részgráfba. (Az alábbi ábrán i=2 és k=8.)
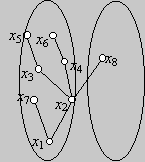
Ha G-nek n pontja van, akkor az eljárás pontosan az n-edik lépésben ér véget és az első lépés kivételével minden lépésben a G gráf egy új élét választja ki és veszi hozzá G’-höz. Ebből következik:
Az I. eljárással kapott G’ részgráf a G gráf összes pontját tartalmazza. Ha G-nek n pontja van, akkor G’-nek n–1 éle van.
