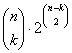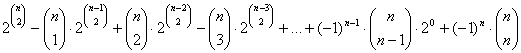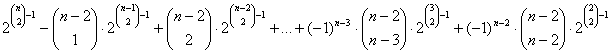Mielőtt a megoldáshoz kezdenénk, bevezetünk néhány elnevezést. A csapatok legyenek a gráf csúcsai, két pont között akkor vezessen él, ha a megfelelő két csapat már játszott egymással. Ezek szerint azt a kérdést tehetjük fel, hogy két pont között vezet-e él. A cél az, hogy kiderítsük, van-e a gráfban telített pont, azaz olyan csúcs, amely az összes többivel össze van kötve. Természetesen a megbeszélést azzal kezdtük, hogy kevesebb szögpontú gráfokkal próbálkoztunk. A feladatot most rögtön általánosan, n csapat (csúcs) esetére oldjuk meg.
Az persze világos, hogy ha minden csúcspárról tudjuk, hogy van-e köztük él, akkor tudjuk, hogy van-e telített pont a gráfban. A kérdés az, hogy szükség van-e az összes él lekérdezésére, vagy minden esetben
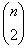
-nél kevesebb kérdéssel is meg tudjuk oldani a problémát.
A válaszhoz szükségünk lesz a következő két állítás valamelyikére.
Az állításra két bizonyítást adunk.
I. BIZONYÍTÁS:
Először a logikai szitát használjuk. Mivel a gráf csúcsait megkülönböztetjük egymástól, ezért
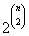
gráf van. n telített pontot tartalmazó gráfból csak egy van, a teljes gráf. A k (0 < k < n) telített pontot tartalmazó gráfok száma
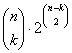
, hiszen a kiválasztott k csúcsból induló összes élnek szerepelnie kell, a többi (n – k) csúcs közötti él pedig egymástól függetlenül vagy szerepel, vagy nem. Persze a k-nál több telített pontot tartalmazó gráfokat többször is számoltuk. Ezek alapján a telített pontot nem tartalmazó gráfok száma:
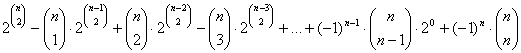
.
Az összeg minden tagja az utolsó kettő kivételével páros. Ezért az összeg paritása megegyezik az utolsó két tag, azaz ± (n – 1) paritásával. Pontosan ezt akartuk belátni.
2. állítás:
Azon gráfok száma, melyeknek n csúcsa van, melyekben két rögzített pontot nem köt össze él, melyekben továbbá nincs telített pont, páratlan.
Erre az állításra is kétféle bizonyítást adunk.
Először a logikai szitát használjuk. A gráfok megszámlálása az előzőeknek megfelelően történik, azonban figyelembe kell vennünk, hogy a két rögzített pontunk, melyek között nem fut él, nem lehet telített pont. Így a kérdéses gráfok száma:
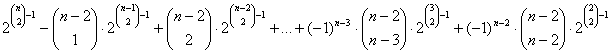
Az összeg minden tagja az utolsó kivételével páros, az utolsó tag pontosan 1 abszolút értékű, így az összeg páratlan. Ezt akartuk igazolni.
II. BIZONYÍTÁS:
Másodjára csoportosítjuk a gráfokat. Legyen A és B a két pont, amelyeket nem köt össze él. Az A csúcsot töröljük a gráfból a belőle induló élekkel együtt. A maradék (n – 1) csúcsú gráfnak lehet 0, 1, ... , (n – 2) vagy (n – 1) telített pontja. Pontosan (n – 2) nem lehet. Ha nincs benne telített pont, akkor az A csúcsot visszatéve a B pont kivételével bármely másik ponttal összeköthetjük. Az így keletkező gráfok száma ezért páros. Ha az (n – 1) szögpontú gráfnak 1, 2, ... , (n – 3) telített pontja van, akkor az A pontot újra figyelembe véve azt a telített pontokkal és B-vel nem szabad összekötni, a maradék pontokkal viszont vagy összekötjük vagy nem. Mivel a pontosan k telített csúcsot tartalmazó gráfokat számoljuk, ezért a B ponton kívül még legalább egy pont nem telített, következésképpen legalább egy élnél két lehetőségünk van. Így ezen gráfokból is páros sok gráf keletkezik. Végül tekintsük a teljes (n – 1)-est! Az A pont most csak izolált pont lehet, tehát még egy gráf van. Összegezve a fentieket azt kapjuk, hogy a keresett gráfok száma páratlan.
Végül visszatérünk az eredeti feladathoz. Megmutatjuk, hogy van olyan eset, amikor szükség van az összes kérdésre.
Képzeljük el a feladatot úgy, hogy mi vagyunk a válaszadók, s partnerünk kérdez. Azt fogjuk belátni, hogy van olyan gráf, amikor valamennyi él létezését meg kell kérdeznie, azaz van olyan eset, amikor
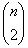
kérdést kell feltennie. Indirekten okoskodunk. Partnerünk első kérdésére nem-et fogunk válaszolni. Ezt az általánosság megszorítása nélkül megtehetjük, amennyiben nem a teljes gráfra gondoltunk. Tegyük most fel, hogy minden esetben partnerünk
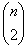
kérdésnél kevesebbel ki tudta deríteni, hogy van-e telített pont a gráfban. Mindegyik kérdéssorozat végén partnerünkkel együtt tudjuk, hogy magát a gráfot nem ismeri, de az eredeti kérdést megválaszolta. Hány gráf jöhet ilyenkor szóba? A meg nem kérdezett élek mindegyike vagy be van húzva a gráfban, vagy nem, tehát páros sok gráf maradt meg. Ezek mindegyikében vagy van telített pont, vagy nincs egyikben sem. Azaz mindegyik „rövid” (
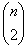
-nél kevesebb kérdésből álló) kérdéssorozattal páros sok olyan gráfot térképeztünk fel, amelyben van telített pont. Ez ellentmondás, hiszen páratlan sok olyan gráf van, amely egy adott élt nem tartalmaz, s van telített pontja. Ezzel a bizonyítást befejeztük.
Most szeretnénk elérni, hogy partnerünk valóban feltegye mind az
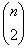
kérdést. A cél elérése érdekében kicsit becsapjuk partnerünket: nem döntjük el előre, hogy melyik gráfra gondolunk, hanem a kérdések közben a még szóbajöhető gráfokat tartjuk számon, s csak az utolsó lépésben „gondolunk” egy gráfra. Taktikánk a fenti bizonyításból kiolvasható. Az első kérdésre nemet válaszolunk, ekkor páratlan sok olyan gráf van, amely tartalmaz telített pontot. Amikor partnerünk a következő kérdést felteszi, akkor gyorsan megnézzük, hogy melyik esetben marad páratlan sok, telített pontot tartalmazó gráf: ha igennel, vagy ha nemmel válaszolunk. Válasszuk azt a feleletet, amely páratlan sok, telített pontot tartalmazó gráfot hagy meg! Most partnerünk nem tudhatja, hogy a gráf, amelyre „gondoltunk”, tartalmaz-e telített pontot, hiszen neki páros sok gráf között kell keresgélnie, ezek közül páratlan sok tartalmaz telített pontot, páratlan sok pedig nem tartalmaz telített pontot, tehát nem tudja a kérdést eldönteni. A következő kérdés feltétele után kövessük a fenti taktikát mindaddig, míg csak két gráf marad!
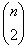
–1 kérdés után eljutunk odáig, hogy már csak két gráf marad, ezek csupán egyetlen élben különböznek egymástól, s egyikük tartalmaz, másikuk nem tartalmaz telített pontot. Partnerünk kénytelen feltenni az utolsó kérdést is. Most eldöntjük, melyik gráfra „gondoltunk”, s ennek megfelelően válaszolunk. Ezzel kikényszerítettük, hogy partnerünk a gráf minden élére rákérdezzen.
Még egy algoritmust adunk arra, hogyan lehet elérni, hogy az összes kérdést feltegye partnerünk. Minden esetben amikor lehet nemet fogunk válaszolni. Mikor kell vigyázzunk? Ha az A és B pontok közötti élről már kiderült, hogy nincs a gráfban, A és C közötti élről még semmit sem tud partnerünk, és most arra kíváncsi, hogy a B és C pontok össze vannak-e kötve, akkor csak igennel válaszolhatunk. Ugyanis A-ról és B-ről már tudja, hogy nem telített pont; ha most nemmel válaszolnánk, akkor C sem lehetne telített, így nem fogja megkérdezni, hogy A és C között van-e él. Kicsit általánosabban: tekintsük azoknak a pontoknak a halmazát, amelyről már kiderült, hogy nem lehet telített. Ha ezek között van két pont, amelyek között futó élre még nem kérdezett rá partnerünk, akkor már nem is fog, azaz nem fogja feltenni az összes kérdést. A válaszadásnál arra kell figyeljünk, hogy ezt a szituációt elkerüljük.
Az első kérdésre nemmel felelünk. Jelöljük T-vel azon pontok halmazát, melyekről már kiderült, hogy nem lehet telített. T-nek most két eleme van, a köztük futó él létezését megkérdezte partnerünk. T-t úgy tudjuk új ponttal bővíteni, ha egy kérdésre nemmel válaszolunk. T-t abban a pillanatban fogjuk egy új P ponttal bővíteni, amikor a T elemei és P közötti élek létezését firtató utolsó kérdés elhangzik, minden egyéb esetben igennel felelünk. P-ről nem derülhet ki, hogy telített pont, hiszen T nem üres, s P és T „utolsó” eleme között nem fut él. P-t is bevesszük a halmazba. Az új T halmaz továbbra is rendelkezik azzal a tulajdonsággal, hogy az elemei között futó összes élre rákérdezett partnerünk. Minden kérdés előtt a fentieket kell mérlegelni, s T-t vagy bővítjük, vagy nem. Az algoritmus csak akkor áll meg, amikor T már (n – 1) pontot tartalmaz, s az egyetlen külső pontból induló (vagy nem induló) utolsó élre kérdez rá társunk. Ezzel elértük, hogy valamennyi kérdést feltegye.
![]()