Árki Tamás és Hraskó András
Kísérletező geometria
Készült a Közoktatási Modernizációs Közalapítvány (KOMA) támogatásával
| A(z) szv002 kódszámú óra |  | |
| Javasolt évfolyam: | 11-12. | |
| Segédeszköz: | Számítógép, Cabri, Euklidesz, Maple, Mathematic, Derive, | |
| Előző óra: | szv001 óra | |
| Következő óra: | szv003 óra | |
Feladatok
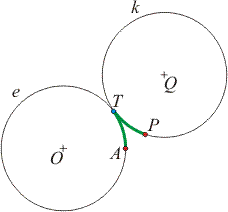
Egy kör (k) alakú kerék csúszás nélkül gördül egy ugyanakkora sugarú rögzített kör (e) körül. Rajzoljuk meg a mozgó kör kerülete valamely pontjának pályáját.
 |
|
szv00201_fel_a. ábra.
|
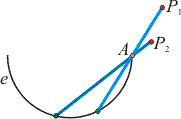
r sugarú félkör alakú gödörben lecsúszik egy 2r hosszúságú pálca (a pálca alsó végpontja a körön fut, közben nekitámaszkodik a félkör A végpontjának). Hol mozog a pálca felső végpontja?
 |
|
szv00202_fel_a. ábra.
|
Rajzoljuk meg a komplex egységkör képét a z → 2z - z2 transzformációnál!
Előzetes megjegyzés, segítség, megoldás és folytatási javaslat kérése
Házi feladatok
Vizsgáljuk tetszőleges hosszúságú pálca lecsúszását félkör alakú gödörben!
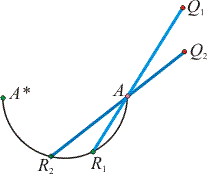
a) Adott az r sugarú e kör AA* félköre, továbbá a d szakasz. Mérjük fel a félkör R pontjából a d-vel egyenlő hosszúságú szakaszt az RA félegyenesre R-től A felé! Rajzoljuk ki az így adódó szakaszok végpontjának mértani helyét!
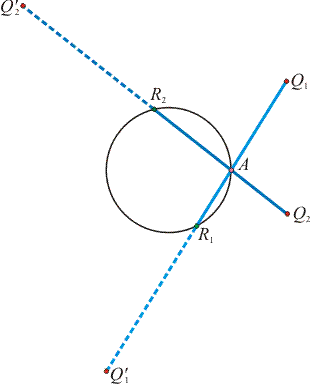
b) Futtassuk R-t a teljes e körön és d-t mérjük fel az RA egyenesre mindkét irányban! Jelenítsük meg az így adódó végpontok mértani helyét is!
 |
 |
|
szv00202b_fel_a. ábra.
|
szv00202b_fel_b. ábra.
|
Előzetes megjegyzés, segítség, megoldás és folytatási javaslat kérése