A 2002-2003 tanévi 11-12-es FPI tehetséggondozó szakkör 19. foglalkozása
Kódok
Összeállította Hraskó András és Szőnyi Tamás
5. szakkör
Folytattuk a Kódok feladatgyűjtemény feldolgozását.
Bemelegítésként a Pénzes barkochbával foglalkoztunk, majd ismétlésként
megoldottuk a 4.11 feladatot. "Kitöltöttünk" 310
szelvényt, amelyekkel a 13-as totón biztosan elérünk 12 vagy 13 találatot.
Ennek kapcsán megismerkedtünk a tökéletes kód, valamint a bináris és a ternér Hamming-kód
fogalmával. Leellenőriztük a Golay-kódok paramétereit. A "Jó
30-as" feladat folytatásaként, a Hétszögminták előkészítése
kedvéért megkerestük az "Ideális 101-es" sorozatokat.
Házi
feladatnak a múlt
óráról megmaradt: hétszögminták, 5.11, új példa: Általános
Hamming-kód, "Ideális 1001-es".
Pénzes barkochba
(Pósa Lajos feladata)
Az 1, 2, 3, ... 16 számok
közül kell kitalálni egyet barkochba-kérdésekkel. A válaszokért fizetnünk kell:
az IGEN válaszért 1 Ft-ot, a NEM válaszért 2-t. Legalább hány Ft-ra van szükség
ahhoz, hogy biztosan kitaláljuk a gondolt számot?
Megoldás
Fordítsuk meg a kérdést!
Próbáljuk meg kitalálni, hogy n Ft felhasználásával legfeljebb hány
dolgot tudunk megkülönböztetni, azaz legfeljebb hány szám közül tudjuk biztosan
kitalálni a gondoltat. Jelölje ezt a számot sn. Ha adott egy sn
elemből álló S halmaz, akkor első kérdésünk két részre osztja S-t:
az I részhalmaz azokból az elemekből áll, amelyekre - mint gondolt
számokra - "igen" a válasz, az N részhalmaz pedig azokból,
amelyekre "nem" a válasz. Ha "igen" választ kapunk, akkor
még (n - 1) Ft maradt meg kérdésekre, "nem" válasz esetén
azonban csak (n - 2), így
|I| = sn-1,
|N| = sn-2, azaz sn = sn-1
+ sn-2. Világos, hogy s1
= 1, míg s2 = 2, így s3 = 3, s4
= 5, s5 = 8, s6 = 13, s7
= 21, tehát 16 szám közül 7 Ft-tal tudjuk biztosan kitalálni a gondolt számot.
Az első kérdésünk lehet pld ez: "a gondolt szám az {1, 2, 3 ..., 13}
halmazban van?".
4.11
Bizonyítsd be, hogy egy kód pontosan akkor
a) k-hiba javító, ha minimális
távolsága legalább 2k+1;
b) k-hiba jelző, ha minimális
távolsága legalább k+1;
c) k-törlés javító, ha k-hiba
jelző!
Megoldás
a) Ha bármelyik két kódszó minimális távolsága legalább (2k+1),
akkor bármelyik kódszóban k betűt elrontva, attól csak k Hamming
távolságra jutunk, míg az összes többitől legalább (k+1) Hamming
távolágnyira leszünk. Így a szó kijavítható.
Ha két kódszó távolsága csak
2k lenne, akkor azokat a szavakat nem tudnánk kijavítani, amely a 2k
hely közül k helyen az egyik kódszóval, k helyen a másik
kódszóval, a többi helyen pedig mindkét kódszóval megegyeznek. Ezek a szavak
mindkét kódszóból megkaphatók k betű elírásával.
b) Ha bármelyik két kódszó távolsága legalább (k+1),
akkor hiába rontunk el egy kódszót k, vagy annál kevesebb helyen, nem
kapunk másik kódszót, hanem tudni fogjuk, hogy hiba történt. Másrészt, ha van
két olyan különböző kódszó, amelyek távolsága legfeljebb k, akkor az
egyiket legfeljebb k helyen "elírva" megkaphatjuk a másikat,
és ilyenkor nem veszi észre a hibát a rendszer.
c) Használjuk fel a b) állítást! Ha a két kódszó távolsága
legfeljebb k, akkor az egyik kódszóból azt a legfeljebb k betűt
törölve, ahol különböznek, olyan "szó"-hoz jutunk, amelynek
rekonstruálása nem egyértelmű. Tehát k-törlés javító kód minimális
távolsága legalább (k+1).
Ha egy kódszó minden más
kódszótól k-nál több helyen eltér, akkor bármelyik k betűjének
törlődése esetén sem keverhető össze másik kódszóval. Tehát egy legalább (k+1)
minimális távolságú kód egyben k-törlés javító is.
13-as totó "Adjunk meg" 59049 szelvénykitöltést a 13 mérkőzésből álló totón úgy,
hogy biztosan legyen olyan szelvényünk, amely legalább 12 találatos!
Emlékeztetünk rá, hogy az 5.7 feladat megoldásában már megmutattuk, hogy ennyi
szelvényre valóban szükség van. A megoldásból az is kiderül, hogy 59049
szelvény pontosan akkor lesz megfelelő, ha a kitöltések 1-hiba javító kódot
alkotnak, azaz bármelyik két különböző kitöltés Hamming távolsága legalább 3.
Konstrukciónk az 5.9 feladatra adott III. konstrukciót, illetve az azt követő -
az 5.6 feladatra vonatkozó - Megjegyzést követi.
Konstrukció
Lineáris kódot keresünk, azaz olyan
a1ˇ y1
+ a2ˇ y2 + ... + a13ˇ
y13 = 0,
b1ˇ y1
+ b2ˇ y2 + ... + b13ˇ
y13 = 0,
c1ˇ y1
+ c2ˇ y2 + ... + c13ˇ
y13 = 0
alakú egyenletrendszert, amelynek egyenletei, változói, műveletei mod 3 értendők. A
kódszavak az egyenletrendszer megoldásai lesznek. Azért van szükség épp három
egyenletre, mert 3
13 szóból csak 3
10-t akarunk kódszónak
választani, azaz a 13 változóból csak 10-et akarunk szabadnak tekinteni, 3
pedig kiküszöbölendő. Láttuk, hogy a kód akkor lesz 1-hiba javító, ha az
együtthatók

mátrixában egyik oszlop sem
azonosan 0, és semelyik két oszlop sem azonos vagy egymás ellentettje (azaz
-1-szerese, vagy másképp: kétszerese). Ilyen mátrixot tudunk választani, hiszen
az oszlopok három elemből álló bináris sorozatok, amelyekből 3
3 = 27
van, az azonosan 0 nélkül 26, az ellentett párokat nem megkülönböztetve épp 13.
Tapasztalataink alapján
kimondhatjuk, hogy az alább definiált kódok 1-hiba javító tökéletes kódok.
Megjegyzés (Bináris és ternér Hamming-kód):
Legyen r tetszőleges
pozitív egész. Az előbbiek általánosításaként értelmezhető egy bináris (tehát
kétféle jelet használó), valamint egy ternér (azaz háromféle jelet használó) lineáris kód. A kódot definiáló egyenletrendszer
egyenleteinek száma mindkét esetben r. A kódszavak hossza a bináris,
illetve a ternér esetben rendre
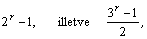
a kódszavak száma pedig
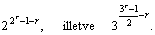
Az egyenletrendszer
egyenleteinek sorrendjét rögzítjük, és így az egyes változók együtthatói
egy-egy
r komponensű bináris, illetve ternér (oszlop)vektort alkotnak.
Ezeket a vektorokat úgy választjuk meg, hogy különbözzenek a nullvektortól,
egymástól, illetve egymás ellentettjeitől (-1-szereseitől).
Tétel (Tietäväinen,
Van Lint) t-hiba javító tökéletes kódból t > 1
esetén csak kettő van, az úgynevezett Golay-kódok, ezek egyike bináris,
3-javító, szavainak hossza 23; a másik ternér, 2-javító, szavainak hossza 11.
A tételt itt nem bizonyítjuk.
A ternér Golay kóddal az 5.7 feladat
táblázatában is találkozunk, hiszen létezése ideális totókulcsot jelent annak
számára, aki a 11 mérkőzésből álló totón legalább 9 találatra tör.
Golay
Ellenőrizzük le, hogy a fenti Tételben említett kódok
adatai megfelelhetnek tökéletes kódnak!
Megoldás
A ternér esetben 11 hosszúságú szóból összesen 311
van. Egy szótól 1 Hamming távolságnyira 2ˇ11=22, míg 2 Hamming távolságnyira 22 ˇ 11ˇ 10/2
= 220 szó van. Egy szótól legfeljebb 2 távolságnyira tehát épp 243=35
szó található. Így nincs kizárva, hogy 311/35 = 36
= 729 kódszóval 2-hiba javító kódot találjunk.
A bináris esetben 23
hosszúságú szóból összesen 223 van. Egy szótól 0, 1, 2, ill. 3 Hamming
távolságnyira rendre
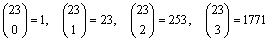
szó van, ami összesen 2048=2
11.
Így nincs kizárva, hogy 2
23/2
11 = 2
12 = 4096
kódszóval 2-hiba javító kódot találjunk.
"Ideális 101-es"
Ebben a feladatban a
természetes számok bizonyos részhalmazait keressük. A számokat mindig kettes
számrendszerben leírva képzeljük, illetve alább így is említjük őket. Két számot
nem a szokásos módon adunk össze, hanem kettes számrendszerbeli alakjuk
megfelelő jegyeit modulo 2, és átvitel nélkül adjuk össze (pld 1100110 + 10011
= 1110101).
A természetes számok
(pontosabban azok kettes számrendszerbeli alakjainak) egy I101
részhalmazát "ideális 101-es"-nek nevezzük, ha
1. Ha h I101-ben van, akkor h0 is I101-ben van; (h0
a h dupláját, tehát azt a számot jelöli, amelyet úgy kapunk, hogy h
mögé írunk egy 0-t)
2. Ha h és j is I101-ban van, akkor h +
j is ott van.
3. 101 is I101-ben van (itt 101 az
egy-nulla-egy számot, azaz az 5-öt és nem a százegyet jelenti).
Hány véges, "ideális
101-es" részhalmaza van a természetes számok halmazának?
Példák
Némi próbálkozás után három példát találhatunk:
A) A természetes számok
halmaza. Ha feltesszük, hogy 1 I101-ben van és alkalmazzuk az 1., 2. szabályokat, akkor ezt a
"részhalmazt" kapjuk.
B) Ha csak annyit teszünk
fel, hogy 101 I101-ben van és alkalmazzuk az 1., 2. szabályokat, akkor egy kisebb
részhalmazt kapunk. Ez pontosan azokból a számokból áll, amelyek kettes
számrendszerbeli alakjában a párosadik helyiértékeken és a páratlanadik helyiértékeken
külön-külön az 1-esek száma páros.
C) Az a részhalmaz is jó,
amelynek elemei az olyan számok, amelyek kettes számrendszerbeli alakjában az
1-esek száma páros. Ezt a részhalmazt az 11 elem "generálja".
Segítség a teljes megoldáshoz: feleltessük meg a természetes
számok kettes számrendszerbeli alakjait F2 testbeli együtthatós
(azaz mod 2 számolunk) polinomoknak! Az a = anˇ2n
+ an-1ˇ2n-1 + ... + a1ˇ21
+ a0ˇ20 = anan-1...a1a0
számnak az anˇxn + an-1ˇxn-1 + ... + a1ˇx + a0 polinom feleljen meg.
Megoldás
A megfeleltetés után már a
polinomok részhalmazait keressük. Az 1. tulajdonság azt jelenti, hogy I101-beli
polinom x-szerese is I101-ben van, 2. szerint pedig I101-beli
polinomok összege is ott van. Ezekből az is következik, hogy I101-beli
polinom tetszőleges polinomszorosa is I101-ben van, hiszen
bármely polinommal való szorzás felépíthető x-szel való szorzásokból és
polinomok összeadásából. Az x4 + x polinommal például
úgy szorzunk meg egy másik polinomot, hogy egymás után négyszer megszorozzuk x-szel
és az eredményhez hozzáadjuk az x-szel szorzott polinomot.
A feladat megoldása innentől
kezdve már nagyon hasonló a "Jó 30-as"
feladatéhoz, csak míg ott az egész számok halmaza volt a főszereplő, itt a
polinomok halmaza játszik. Lényeges közös vonás, hogy mindkét halmazban lehet
maradékosan osztani.
Legyen most I101
legkisebb fokú (az azonosan 0-tól különböző) eleme a p polinom. Ha q is I101-ben van, akkor p|q,
mert a q polinom p-vel való osztási maradéka is I101-ben
van és p-nél kisebb fokú, így 0. Tehát I101 a p
összes többszöröséből, és csakis azokból áll. Annyi megoldás van, ahány osztója
van az x2 + 1 polinomnak. Az osztók: 1, x + 1, x2
+ 1, amiből látható, hogy a fenti A), B) és C) eset az összes megoldást lefedi.
"Ideális 1001-es"
Oldjuk meg az "ideális 101-es"
feladatot 101 helyett mindenütt 1001-gyel!
Hétszögminták
Ebben a feladatban egy
szabályos hétszög csúcsaira írunk 0-t vagy 1-et. Összesen 27=128
ilyen kitöltés van. A kitöltések egy I7 részhalmaza "7-szögre
ideális", ha
1. Ha h az I7-ben van, akkor h bármely (n·360°/7-kal
való) elforgatottja is I7-ben van.
2. Bármely két I7-beli kitöltés csúcsonként és mod 2 számított összege
is I7-ben van.
A kitöltéseknek hány "7-szögre ideális" részhalmaza van?
5.11
Egy kém az
ellenséges ország televíziójánál dolgozik. Esténként alkalma van az adásba
kerülő 8×8-as fekete fehér tábla egyetlen mezőjének színét
megváltoztatni. Nem feltétlenül szükséges változtatnia. Sajnos sohasem tudja
előre, hogy milyen mintázatú lesz a 64 mező, amikor eléje kerül. Hányféle
információt tud így küldeni a TV-n keresztül?
Juhász Istvántól és Szegedy Balázstól is hallottam
